Теорема 1

Якщо і 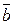колінеарні вектори і , то існує єдине число α таке, що 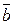=α· (1)

Якщо то доведення очевидне, число α=0 існує і умова теореми виконується: .

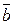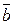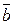Якщо , то ↑↑ або ↑↓ . Враховуючи означення добутку вектора на число, легко підібрати таке число а: якщо вектори співнаправлені то α= | |/| |, а якщо протилежно направлені, то α=- | |/| |.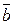

Покажемо, що α - єдине. Припустимо, що існує ще одне число β таке, що 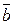=β · . Але тоді α· =β· , або α· -β· =(α-β)· = . Так як за умовою теореми , то (α-β)=0 і α=β.

Зрозуміло, що можна говорити про відношення колінеарних векторів 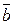/ =α (ділити довільні вектори не можна).