Теорема 6

Кожна координата лінійної комбінації декількох векторів, заданих своїми координатами, являє собою ту ж лінійну комбінацію відповідних координат цих векторів.

Доведення: Нехай вектор 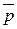є лінійною комбінацією векторів :

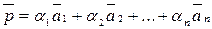і вектори мають координати:

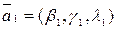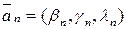, ,…, . Запишемо їх розклади по базису ,

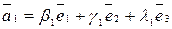,…, і підставимо в розклад вектора : = +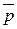

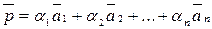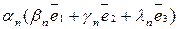+ +…+ . Згрупувавши коефіцієнти біля базисних векторів отримаємо:

Отже, вектор

, що й потрібно було довести.