 |
Главная Случайная страница Контакты | Мы поможем в написании вашей работы! | |
Добуток вектора на число
|
|
Добутком вектора  на дійсне число λ називається такий вектор
на дійсне число λ називається такий вектор 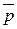 , для якого виконуються умови:
, для якого виконуються умови:
1. | 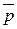 |=| λ | |
|=| λ | |  | – довжина вектора
| – довжина вектора 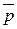 ;
;
2.  ↑↑
↑↑ 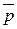 – коли λ >0;
– коли λ >0;
3.  ↑↓
↑↓ 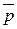 – коли λ <0;
– коли λ <0;
 Властивості:
Властивості:
Для будь-яких дійсних чисел α і β та векторів  ,
, 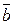 мають місце рівності:
мають місце рівності:
1. 1·  =
=  ; (-1)·
; (-1)·  =-
=-  ;
;
2. α·( +
+ 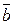 )=α·
)=α·  +α·
+α· 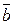 ;
;
3. (α+β)·  =α·
=α·  + β·
+ β·  ; Рис. 4
; Рис. 4
4. α·(β·  )=(α·β)·
)=(α·β)·  .
.
Доведення:
1. Властивість випливає з означення добутку вектора на число.
2. 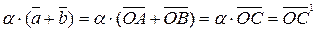 (рис. 4).
(рис. 4).
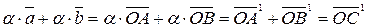 (рис. 4).
(рис. 4).
Отже, ми отримали гомотетію з центром в точці О та коефіцієнтом α. При гомотетії паралелограм АСВО перейшов в паралелограм А1С1В1О, діагональ ОС перейшла в ОС1.
3. Справедливість третьої властивості випливає з того, що вектори α ·  і β ·
і β ·  колінеарні. Їх додавання фактично зводиться до додавання чисел α ·|
колінеарні. Їх додавання фактично зводиться до додавання чисел α ·|  | і β ·|
| і β ·|  | та побудови вектора отриманої довжини, який колінеарний вектору
| та побудови вектора отриманої довжини, який колінеарний вектору  .
.
4. Очевидно, що вектори α·(β·  ) і (α·β)·
) і (α·β)·  співнаправлені, так як в обох випадках добуток чисел α і β має однаковий знак. Покажемо, що і модулі їх рівні. Дійсно, за означенням добутку вектора на число отримаємо:
співнаправлені, так як в обох випадках добуток чисел α і β має однаковий знак. Покажемо, що і модулі їх рівні. Дійсно, за означенням добутку вектора на число отримаємо:
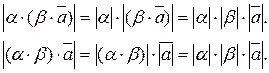
Дата публикования: 2015-09-18; Прочитано: 797 | Нарушение авторского права страницы | Мы поможем в написании вашей работы!
