Нормальное уравнение плоскости

Всякую плоскость можно задать следующими параметрами: длиной перпендикуляра, опущенного из начала координат на плоскость, и направляющими косинусами 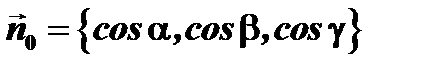этого перпендикуляра.

Пусть – произвольная точка плоскости.

Рассмотрим три вектора: .

Для того, чтобы точка принадлежала данной плоскости, необходимо и достаточно, чтобы векторы и были перпендикулярны, т.е. или

. Следовательно, и

(4)

Уравнение (4) выражает собой условие, при котором точка лежит на данной плоскости, и называется нормальным уравнением этой плоскости.