Векторное произведение двух векторов

Векторным произведением двух векторов и называется новый вектор , длина которого численно равна площади параллелограмма, построенного на векторах и 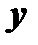, перпендикулярный к плоскости этих векторов и направленный в такую сторону, чтобы кратчайший поворот от к вокруг полученного вектора представлялся происходящим против часовой стрелки, если смотреть из конца вектора (рис.4). Для векторного произведения и приняты обозначения

Векторное произведение обладает следующими свойствами:

1) ;

2) ;

3) ;

4) Из определения векторного произведения следует, что

.

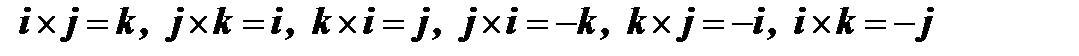5) .

Пусть даны два вектора, разложенные по базису :

.

. Полученное выражение можно записать более компактно, если ввести определитель третьего порядка, у которого первая строка состоит из базисных переменных , вторая строка из координат вектора и третья строка из координат вектора :

(10)