Головні напрямки та головні діаметри. Рівняння осей симетрії

Означення. Два спряжені діаметри лінії другого порядку називають головними, якщо вони взаємно перпендикулярні.

На рисунку 4 головними діаметрами лінії є прямі та . Дослідимо питання, як знаходити головні діаметри.

Оскільки дві прямі з кутовими коефіцієнтами та будуть перпендикулярними при виконанні умови , то, підставляючи у рівність (3) значення , дістаємо

,

звідки отримуємо співвідношення для відшукання коефіцієнта :

. (4)

Одержане рівняння завжди має розв’язки, оскільки його дискримінант . Очевидно, що лише при умовах . У цьому випадку рівняння лінії можна звести до виду , де 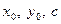– деякі числа. При умові >0 одержане співвідношення задає коло, для якого будь–які два взаємно перпендикулярні діаметри є головними.

Нехай числ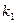а та є коренями рівняння (4). Тоді рівності

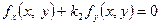, (5)

будуть визначати головні діаметри лінії .

Головні діаметри є осями симетрії лінії. Справді, якщо – деяка хорда лінії та – два її головні діаметри, причому , то відрізок буде ділитися прямою пополам. Отже, точки та симетричні відносно . Тому одержані вище рівняння (5) будуть одночасно рівняннями осей симетрії лінії .

Для відшукання осі симетрії параболи, кутовий коефіцієнт якої, як нам відомо, дорівнює , зауважимо, що вона ділить пополам хорди, що перпендикулярні до неї. Напрямок цих хорд задається кутовим коефіцієнтом . Підставляючи дане число в рівняння , отримаємо, що рівняння осі симетрії параболи має вигляд

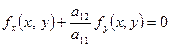. (6)

Вісь симетрії параболи називають її головним діаметром. На рисунку 3 – це пряма .

При необхідності вершину параболи можна знайти, розв’язавши систему рівнянь (1), (6).

Задача 4. Знайти рівняння осей симетрії лінії, заданої рівнянням

.

Розв’язання. Знаходимо , . Рівняння (4) у даному випадку матиме вигляд , звідки . Підставляючи одержані значення у рівняння (5), дістаємо .

Відповідь. , .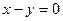

Задача 5. Знайти рівняння осі симетрії та вершину параболи, заданої рівнянням .

Розв’язання. Послідовно знаходимо:

, , .

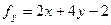Використавши рівняння (6), отримуємо рівняння осі симетрії параболи у вигляді , або 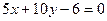. Для відшукання вершини параболи складемо систему рівнянь виду (1), (6):

.

Розв’язуючи її, дістаємо

,

або .

Відповідь. ; .