Центр лінії

Хордою лінії другого порядку назвемо відрізок, який сполучає дві точки на лінії.

Якщо для лінії існує точка, в якій всі хорди, що проходять через неї, діляться пополам, то цю точку називають центром лінії. Фактично центр лінії є її центром симетрії, оскільки разом із будь-якою точкою лінії, їй належить також точка, симетрична даній відносно центра. На рисунку 8 центром лінії є точка – середина всіх можливих хорд, які проходять через неї.

Розглянемо питання відшукання центра лінії, заданої рівнянням (1). Відповідно з попереднім пунктом, умовою того, щоб точка була серединою хорд, що проходить через неї, є виконання рівності . Оскільки вона повинна виконуватися для довільного напрямку, заданого вектором 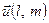, тобто для довільних та , то для відшукання центра лінії дістаємо систему рівнянь

. (4)

Існування та кількість розв’язків системи (4) залежить від визначника .

Якщо , то система (4) має єдиний розв’язок. У цьому випадку лінія має єдиний центр і її називають центральною. Прикладами таких ліній є еліпс, гіпербола, лінія другого порядку, яка вироджується у пару прямих, які перетинаються.

Якщо , то система (4) має безліч розв’язків, або не має жодного. Лінію у цьому випадку називають нецентральною. Прикладами таких ліній є парабола, пара паралельних прямих. В останньому випадку центри лінії утворюють пряму, яка є середньою лінією смужки, утвореної даними паралельними прямими.

Наведемо декілька прикладів.

Приклад 1. Знайти центр лінії, заданої рівнянням

.

Розв’язання. Складемо та розв’яжемо систему рівнянь . Дістаємо

,

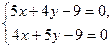звідки . Отже, задана лінія має єдиний центр, який знаходиться в точці .

Приклад 2. Дослідити кількість центрів лінії

у залежності від параметрів та .

Розв’язання. Дістаємо . Тому при та і лінія має єдиний центр.

Система рівнянь тобто при запишеться у вигляді і матиме при безліч розв’язків, а при - жодного.

При отримуємо систему , яка матиме безліч розв’язків при , та жодного при .