Приклади побудови ліній за їхніми рівняннями

Розглянемо на конкретних прикладах задачі на побудову центральних ліній.

Задача 7. Побудувати лінію, задану рівнянням

.

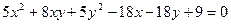Розв’язання. Оскільки 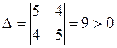, то лінія, яку ми досліджуємо, еліптичного типу. Система для відшукання центра запишеться у вигляді

.

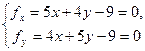Розв’язавши її, знаходимо 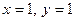. Рівняння осей симетрії було знайдено раніше (задача 4) у вигляді співвідношень 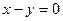, 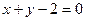. Знайдемо точки перетину лінії з координатними осями. Системи

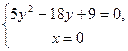та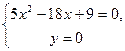

мають розв’язки 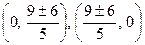, яким відповідають точки

.

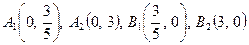Знаходимо точки перетину лінії з осями симетрії. Для цього складаємо системи рівнянь

,

,

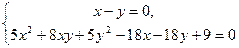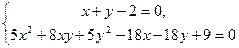звідки дістаємо ще чотири точки на лінії:

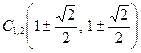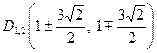, . Знайдені нами прямі та точки дозволяють зобразити лінію (рис. 5).

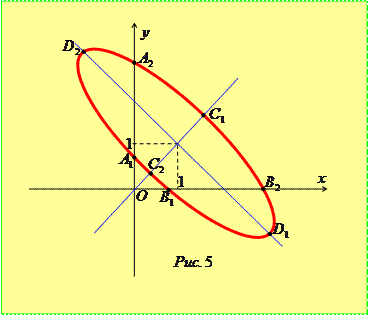
Задача 8. Побудувати лінію, задану рівнянням .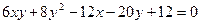

Розв’язання. Встановимо тип лінії. Обчисливши визначник 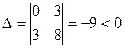, робимо висновок, що лінія гіперболічного типу.

Шукаємо центр лінії. Із системи

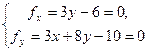
дістаємо 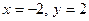. Рівняння осей симетрії шукаємо у виді 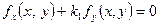, 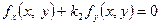. Числа 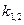знаходимо, як корені рівняння 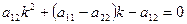, тобто рівняння 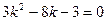. Дістаємо 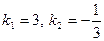. Після очевидних перетворень рівняння осей симетрії запишуться у вигляді .

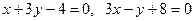Займемось відшуканням рівнянь асимптот. Підставляючи у рівності 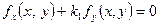, 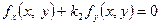замість 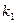та 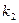корені рівняння 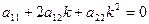(у даному випадку воно запишеться у виді 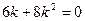і матиме корені 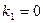, 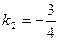), дістаємо рівняння двох асимптот: .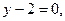

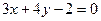Знайдемо точки перетину лінії з координатними осями. Із систем

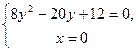та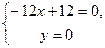

отримуємо точки .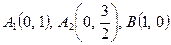

Точки перетину лінії з осями симетрії знаходимо із систем

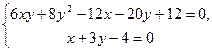та .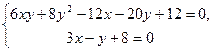

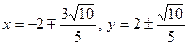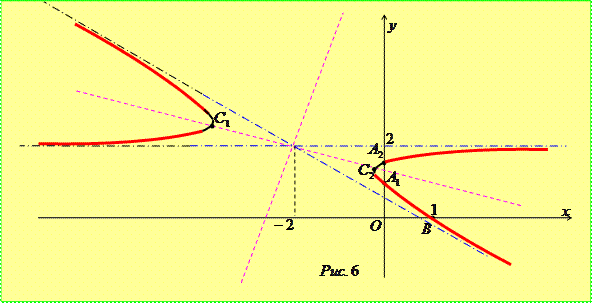
Із першої системи дістаємо , що визначає дві точки 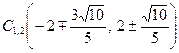. Очевидно, що друга система розв’язків не має, оскільки гіпербола перетинається тільки з одною із своїх осей симетрії. Отримані вище результати дозволяють зобразити лінію (рис. 6).

Задача 9. Побудувати лінію, задану рівнянням .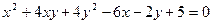

Розв’язання. Встановлюємо тип лінії. Обчисливши визначник 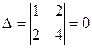, бачимо, що лінія параболічного типу. Шукаємо вісь симетрії. Використавши рівність 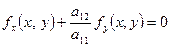та обчисливши 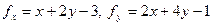, дістаємо рівняння 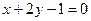. Знайдемо точку перетину лінії із одержаною прямою, тобто вершину параболи. Із системи рівнянь

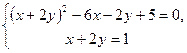
дістаємо 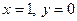. Вісь 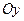задана лінія не перетинає, оскільки при 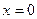рівняння 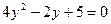не має розв’язків. Система

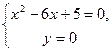
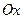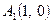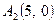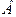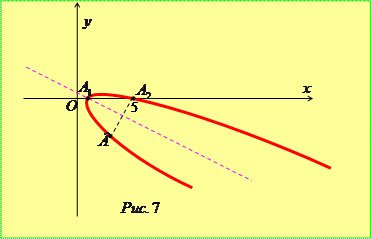
дозволяє знайти дві точки перетину лінії з віссю : та , перша з яких, очевидно, співпадає з вершиною параболи. Зауважимо, що при зображенні лінії можна додатково використати точку , яка симетрична до точки 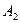відносно осі параболи (рис. 7).

На завершення відмітимо, що розглянутий вище спосіб побудови ліній другого порядку не завжди є ефективним. Зокрема, при необхідності побудови геометричного місця точок, координати яких задовольняють рівняння 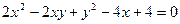, можна виконати необхідні обчислення за вказаною вище схемою та отримати кінцевий результат. В той же час, записавши рівняння у виді 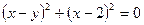, легко бачити, що рівність можлива лише у випадку, коли одночасно виконуються умови 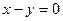та 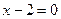, тобто при 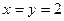. Таким чином, рівняння визначає єдину дійсну точку .

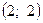Деякі інші способи міркувань, зокрема спрощення рівняння лінії другого порядку за допомогою геометричних перетворень та метод інваріантів будуть розглянуті у наступних лекціях.