 |
Главная Случайная страница Контакты | Мы поможем в написании вашей работы! | |
Перетин лінії з прямою. Частинні випадки
|
|
Перетнемо лінію другого порядку  прямою
прямою  , яка проходить через деяку точку
, яка проходить через деяку точку  та паралельна до вектора
та паралельна до вектора 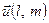 . Параметричні рівняння прямої
. Параметричні рівняння прямої  запишуться у виді
запишуться у виді
 . (2)
. (2)
Для відшукання точок перетину лінії  та прямої
та прямої  , дістаємо систему рівнянь
, дістаємо систему рівнянь
 .
.
Розв’язуючи її, отримаємо квадратне рівняння
 , (3)
, (3)
де
 ,
,



 ,
,
 .
.
Дослідимо особливості взаємного розташування лінії  та прямої
та прямої  у випадках, коли деякі коефіцієнти рівняння (3) рівні нулю.
у випадках, коли деякі коефіцієнти рівняння (3) рівні нулю.
1. Нехай  . Оскільки один із коренів рівняння
. Оскільки один із коренів рівняння  рівний 0, а йому відповідає точка
рівний 0, а йому відповідає точка  , то у цьому випадку одна із точок перетину лінії
, то у цьому випадку одна із точок перетину лінії  та прямої
та прямої  співпадає з точкою
співпадає з точкою  (рис. 1).
(рис. 1).
2. Нехай  і рівняння
і рівняння  має два дійсні корені
має два дійсні корені  . Даним кореням відповідають дві точки перетину
. Даним кореням відповідають дві точки перетину  . Легко бачити, що у цьому випадку точка
. Легко бачити, що у цьому випадку точка  є серединою хорди
є серединою хорди  (рис. 2).
(рис. 2).


3. Нехай  . Рівняння
. Рівняння  має єдиний корінь
має єдиний корінь  . Дослідимо, як змінюється другий корінь рівняння (3) при
. Дослідимо, як змінюється другий корінь рівняння (3) при  . Маємо
. Маємо
 .
.
Очевидно, що при  один із коренів рівняння прямує до
один із коренів рівняння прямує до  , а абсолютна величина другого – до
, а абсолютна величина другого – до  . Згідно із рівностями (2) при
. Згідно із рівностями (2) при  одна із точок перетину нескінченно віддаляється від точки
одна із точок перетину нескінченно віддаляється від точки  . Таку точку ми будемо позначати
. Таку точку ми будемо позначати  та говорити, що пряма перетинає лінію в нескінченно віддаленій точці. Напрям прямої
та говорити, що пряма перетинає лінію в нескінченно віддаленій точці. Напрям прямої  при цьому будемо називати асимптотичним. Асимптотичним буде, наприклад, напрям прямої, яка перетинає параболу та проведена паралельно до її осі симетрії (рис. 3).
при цьому будемо називати асимптотичним. Асимптотичним буде, наприклад, напрям прямої, яка перетинає параболу та проведена паралельно до її осі симетрії (рис. 3).
 4. Випадок
4. Випадок  є поєднанням випадків 1 та 2. Рівняння (3) матиме вид
є поєднанням випадків 1 та 2. Рівняння (3) матиме вид  та корені
та корені  . Пряма
. Пряма  буде дотикатись до лінії
буде дотикатись до лінії  у
у 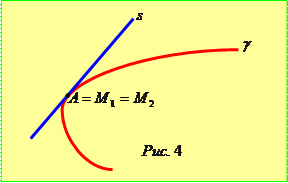 точці
точці  (рис. 4).
(рис. 4).
 5. При
5. При  точка
точка  належить лінії
належить лінії  , а пряма
, а пряма  матиме відносно
матиме відносно  асимптотичний напрям (рис. 5).
асимптотичний напрям (рис. 5).
 6. Якщо
6. Якщо  , то рівняння (3) не має розв’язків. У цьому випадку пряма
, то рівняння (3) не має розв’язків. У цьому випадку пряма  не має з лінією спільних точок та має відносно
не має з лінією спільних точок та має відносно  асимптотичний напрям (рис. 6).
асимптотичний напрям (рис. 6).
 7. Коли
7. Коли  , то рівняння (3) має розв’язком довільне дійсне число
, то рівняння (3) має розв’язком довільне дійсне число  . Тоді кожна точка прямої
. Тоді кожна точка прямої  належить лінії
належить лінії  . Це можливо, наприклад, коли лінія
. Це можливо, наприклад, коли лінія  вироджується у пару прямих (рис. 7).
вироджується у пару прямих (рис. 7).
Дата публикования: 2015-09-17; Прочитано: 809 | Нарушение авторского права страницы | Мы поможем в написании вашей работы!
