Поняття загального рівняння лінії другого порядку

Лекція 18. Загальне рівняння лінії другого порядку

План

Поняття загального рівняння лінії другого порядку.

Перетин лінії з прямою. Частинні випадки.

Центр лінії.

Рівняння дотичної та нормалі.

Поняття загального рівняння лінії другого порядку.

Розглянемо алгебраїчну лінію другого порядку , задану рівнянням

, (1)

де – деякі дійсні числові коефіцієнти, причому коефіцієнти одночасно не дорівнюють нулю. Доданки називають групою старшихчленів, вираз – лінійною частиною, число – вільним членом рівняння. Розв’язки даного рівняння, тобто упорядковані пари чисел на координатній площині задають певну множину точок, які утворюють, взагалі кажучи, деяку лінію. З частинними випадками такого рівняння ми уже зустрічалися раніше. Наприклад, рівняння 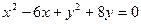або задає коло з центром в точці , радіус якого 5, рівняння визначає гіперболу з дійсною піввіссю 3 та уявною піввіссю 2, а рівняння задає єдину точку , що стає очевидним, якщо це рівняння записати у виді .

Рівняння (1) називають загальним рівнянням лінії другого порядку. З нього можна отримати будь-яке конкретне рівняння другого порядку. Зокрема в останньому прикладі . Виділення в деяких коефіцієнтах загального рівняння множника 2 зроблено для зручності та стане зрозумілим дещо пізніше.

Оскільки рівняння (1) містить 6 коефіцієнтів, які визначаються з точністю до сталого множника, то лінія другого порядку задається, взагалі кажучи, 5точками. В окремих випадках кількість умов, що визначають лінію другого порядку, може бути меншою. Наприклад, коло задається трьома точками, взятими на ньому, парабола, як виявиться дальше, – чотирма.

З метою компактності записів в подальшому введемо в розгляд символи , означивши їх рівностями

,

а також

.

Вони не є складними для запам’ятання. Зокрема можна трактувати, як половину похідної від функції по змінній , вважаючи при цьому змінну сталою, а – як половину похідної від функції по змінній при умові, що не змінюється.

В (1) за допомогою співвідношень , перейдемо до нових змінних . Рівняння лінії набуде вигляду

(*)

і стає однорідним. Відповідно його називають рівнянням лінії другого порядку в однорідних координатах. Змінні при цьому називають однорідними координатами.

Ліва частина рівняння, являючи собою суму доданків другого степеня, утворює так звану квадратичну форму. Такі конструкції є об’єктом детального дослідження курсу лінійної алгебри, що дозволяє отримані там результати застосувати при вивченні властивостей ліній другого порядку, що буде використано нами дещо пізніше.

Якщо ввести позначення

,

,

,

то рівняння (*) можна подати у вигляді

.

Відмітимо, що отримане, симетричне відносно усіх трьох змінних, співвідношення називають формулою Ейлера.

Найближчими нашими задачами буде дослідження властивостей ліній, заданих рівнянням (1), вивчення особливостей їх розташування відносно системи координат, а також дослідження питання, скільки та які різні види ліній може визначати рівняння (1).