 |
Главная Случайная страница Контакты | Мы поможем в написании вашей работы! | |
Геометричний зміст знаку виразу . Пряма яка розглядається в деякій афінній системі координат , розбиває площину на дві півплощини з границею d
|
|
 Пряма
Пряма 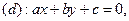 яка розглядається в деякій афінній системі координат
яка розглядається в деякій афінній системі координат 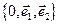 , розбиває площину на дві півплощини з границею d. Встановимо умови, які визначають ці півплощини. Насамперед відмітимо, що вектор
, розбиває площину на дві півплощини з границею d. Встановимо умови, які визначають ці півплощини. Насамперед відмітимо, що вектор 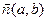 не може бути паралельним до прямої
не може бути паралельним до прямої 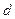 . Справді, нам відомо, що вектор
. Справді, нам відомо, що вектор 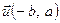 паралельний до прямої. Тоді якби вектори
паралельний до прямої. Тоді якби вектори 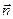 та
та 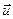 були колінеарними, то виконувалася б рівність
були колінеарними, то виконувалася б рівність 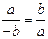 , або
, або 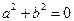 , що неможливо, оскільки коефіцієнти
, що неможливо, оскільки коефіцієнти 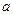 та
та 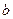 в рівнянні прямої одночасно не можуть дорівнювати нулю. Обчислимо значення виразу
в рівнянні прямої одночасно не можуть дорівнювати нулю. Обчислимо значення виразу 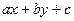 для довільної точки
для довільної точки 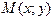 , яка не належить прямій
, яка не належить прямій 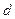 . Для цього через точку
. Для цього через точку 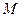 проведемо пряму паралельно до вектора
проведемо пряму паралельно до вектора 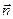 та позначимо точку її перетину з прямою
та позначимо точку її перетину з прямою 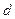 через
через 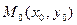 (рис. 8). Із колінеарності векторів
(рис. 8). Із колінеарності векторів 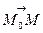 та
та 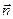 тобто з рівності
тобто з рівності 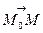
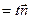 випливають співвідношення
випливають співвідношення 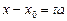 ,
, 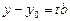 . Тому
. Тому
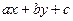
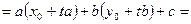
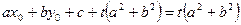 .
.
Отже, знак виразу 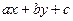 залежить тільки від знаку числа
залежить тільки від знаку числа  . При
. При 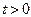 вектори
вектори 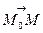 та
та 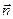 співнапрямлені, тому точки, для яких має місце нерівність
співнапрямлені, тому точки, для яких має місце нерівність 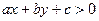 утворюють одну півплощину, а при
утворюють одну півплощину, а при  вектори напрямлені протилежно, тому точки, для яких виконується нерівність
вектори напрямлені протилежно, тому точки, для яких виконується нерівність 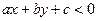 , будуть утворювати іншу півплощину з границею
, будуть утворювати іншу півплощину з границею 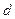 .
.
Дата публикования: 2015-09-17; Прочитано: 1611 | Нарушение авторского права страницы | Мы поможем в написании вашей работы!
