Відстань від точки до прямої

Розглянемо на площині деяку пряму та точку і поставимо задачу, як, знаючи рівняння прямої та координати точки у деякій прямокутній системі координат, знайти відстань від точки до прямої (дану відстань дальше будемо позначати . Нехай пряма задана рівнянням , а точка своїми координатами: 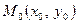. Нехай точка H – основа перпендикуляра, опущеного з точки на пряму та координатами точки H є деякі числа та : (рис. 1). Вектор перпендикулярний до прямої , тому він колінеарний вектору . Із колінеарності векторів та 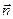дістаємо , , або . Оскільки точка H належить прямій d, то виконується рівність , звідки

.

Тоді

.

Таким чином,

.

Одержане співвідношення називають формулою відстані від точки до прямої.