Примеры решения задач. 6.2.1.Дана матрицалинейного оператора

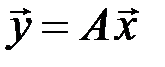6.2.1. Дана матрицалинейного оператора . Записать равенство в координатной форме.

◄ По определению (формула (6.2))

►

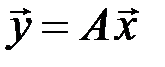
6.2.2. Найти вектор , в который линейный оператор преобразует вектор .

◄ Линейный оператор преобразует вектор в его образ

. ►

6.2.3. Найти собственные значения и собственные векторы линейного оператора (матрицы) .

◄ Собственные значения находим из характеристического уравнения (6.4):

,

корни которого и .

Система (6.3) для нахождения координат и собственных векторов в рассматриваемом случае имеет вид

(6.5)

Подставим в нее :

Полагая – произвольным, находим . Таким образом, векторы , где – собственные векторы, соответствующие собственному значению , то есть (рис 6.2).

Подставим в (6.5) :

Полагая – произвольным, находим . Таким образом, векторы , где – собственные векторы, соответствующие собственному значению , то есть (рис 6.2).

Возьмем и разложим произвольный вектор по базису из векторов , : . Тогда его образ

,

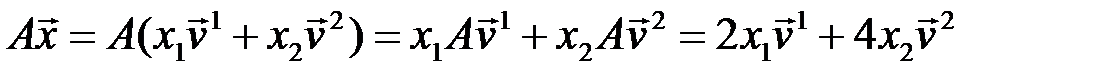то есть действие оператора на произвольный вектор состоит в «растяжении» его по направлениям собственных векторов и , соответственно в и раз (рис 6.2). ►

Рис. 6.2. Действие оператора на параллелограмм, построенный на собственных векторах.