Понятие линейного оператора

Пусть 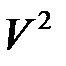– линейное пространство (геометрических) векторов на плоскости. Фиксируем базис 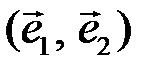в 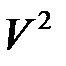и будем отождествлять вектор 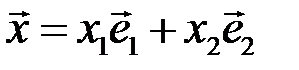с арифметическим вектором-столбцом: .

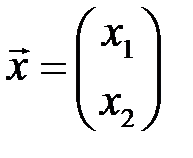Каждая квадратная матрица второго порядка 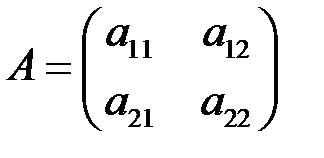определяет линейный оператор в линейном пространстве 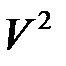– преобразование, ставящее в соответствие каждому вектору 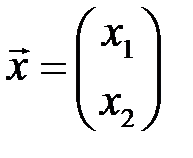вектор 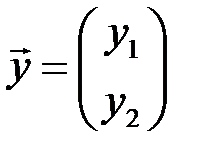по правилу

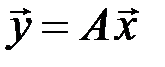
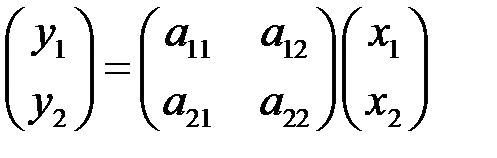
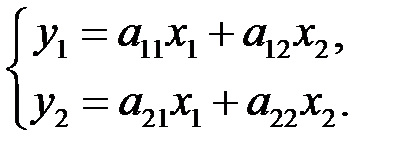(6.1)

Вектор 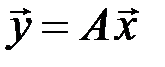называется образом вектора .

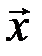Если считать, что начало каждого вектора находится в одной точке , то линейный оператор можно рассматривать и как преобразование точек плоскости, преобразующее конец вектора 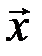в конец его образа .

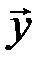Аналогично, квадратная матрица 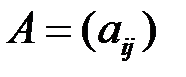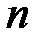-го порядка определяет линейный оператор в 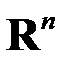– преобразование, ставящее в соответствие каждому вектору-столбцу вектор-столбец по правилу

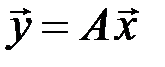
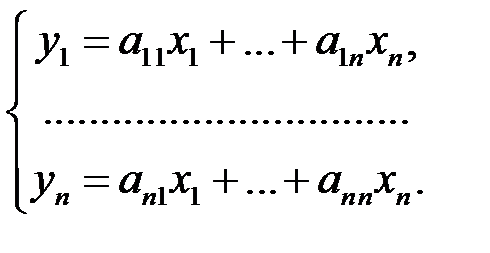
Точно так же, как мы отождествляем при фиксированном базисе вектор с его координатным столбцом, будем отождествлять линейный оператор с задающей его матрицей.