Геометрические приложения скалярного произведения

Через скалярное произведение, а потому и через координаты можно выразить длину вектора и угол между векторами. Приведем выражения для векторов в пространстве. Для векторов на плоскости формулы аналогичны.

Из (8.2) и (8.6) получаем выражение для длины вектора:

, (8.7)

а из (8.1), (8.6) и (8.7) выражение для косинуса угла между векторами:

. (8.8)

Из (8.1) также следует условие ортогональности (взаимной перпендикулярности) векторов:

. (8.9)

Рис. 8.1.

A

B

A 1

B 1

Ортогональной проекцией вектора на направление вектора (рис.8.1) называется число

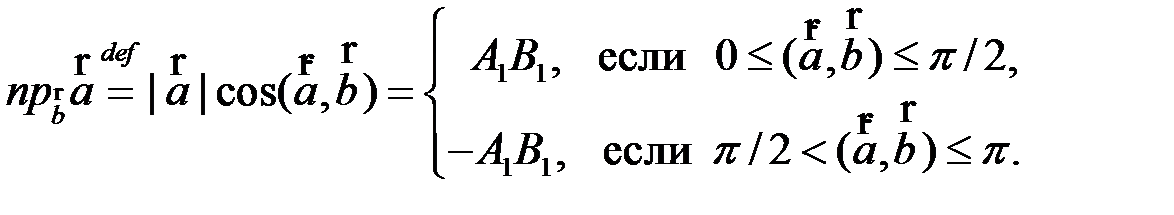
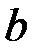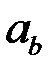Иногда ее называют проекцией вектора на ось (направленную прямую, направление на которой задается вектором ) и обозначают ее . Например проекция вектора на ось : .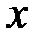

Из (8.8) получаем выражение для ортогональной проекции через скалярное произведение:

. (8.10)

Координаты вектора 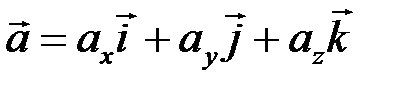в ортонормированном базисе являются его проекциями на направления базисных векторов (на оси координат):

, , , (8.11)

Рис. 8.2

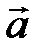
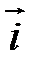
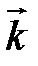
где , , (рис. 8.2).

Величины 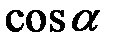, , и называют направляющими косинусами вектора . Вектор

является единичным вектором () в направлении вектора . Он называется ортом вектора , а его нахождение – нормированием вектора .

Так как , то

. (8.12)