Задачи для самостоятельного решения. 5.3.1.Дан параллелограмм с центром в точке O

5.3.1. Дан параллелограмм 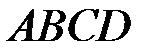с центром в точке O. Выразить векторы , , , , , через векторы и .

5.3.2. В трапеции 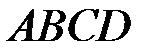длина основания в три раза больше длины основания . Выразить векторы , , , через векторы и .

В задачах 5.3.3-5.3.4вектор задан координатами в ортонормированном базисе. Записать разложение по этому базису. Сделать рисунок.

5.3.3. в базисе на плоскости.

5.3.4. в базисе в пространстве.

В задачах 5.3.5-5.3.6найти векторы , , .

5.3.5. , .

5.3.6. , .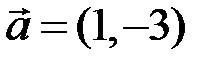

В задачах 5.3.7-5.3.8 выяснить, коллинеарны ли векторы и , и . Если они коллинеарны, то найти линейную зависимость между ними.

5.3.7. , , .

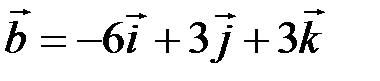5.3.8. , , .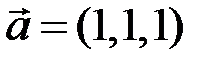

В задачах 5.3.9-5.3.11убедиться, что векторы , , линейно зависимы. Найти эту зависимость. Является ли вектор линейной комбинацией векторов , ?

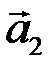5.3.9. , , .

5.3.10. , , .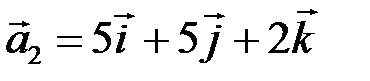

5.3.11. , , .

В задачах 5.3.12-5.3.13 выяснить, компланарны ли векторы , и .

5.3.12. , , .

5.3.13. , , .

В задачах 5.3.14-5.3.15 убедиться, что векторы образуют базис, и разложить вектор по этому базису.

5.3.14. , , .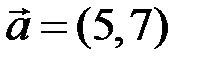

5.3.15. , , .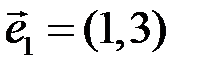

В задачах 5.3.16-5.3.17 убедиться, что векторы 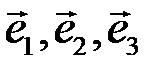образуют базис, и разложить вектор по этому базису.

5.3.16. , , , .

5.3.17. , , , .

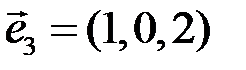5.3.18. Пользуясь определением, доказать, что векторы-строки длины

,

,

……………………..

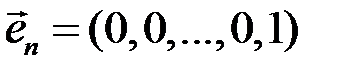
образуют базис в . Он называется каноническим базисом .

5.3.19. Пользуясь определением и теоремой Крамера, доказать, что арифметические векторы , , образуют базис в , если определитель, составленный из них как строк, отличен от нуля.

5.3.20. Доказать, что при любом функции , ,…, , , линейно независимы.

5.3.21. Доказать, что множество всех многочленов от одной переменной степени с «обычными» операциями сложения и умножения на действительное число является линейным пространством.

5.3.22. Доказать, что множество целых чисел с «обычными» операциями сложения и умножения на действительное число не является линейным пространством.