Определение. Свойства. Вычисление

Скалярным произведением (геометрических) векторов и называется число, равное произведению длин этих векторов на косинус угла между ними:

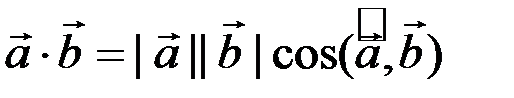. (8.1)

Свойства скалярного произведения: для любых векторов , , и для любого числа

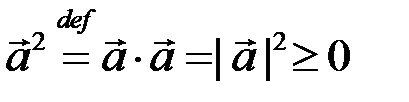; (8.2)

; (8.3)

; (8.4)

. (8.5)

Выражение скалярного произведения через координаты сомножителей в ортонормированном базисе: Если

, ,

то

. (8.6)

В задачах этого раздела, если базис, в котором заданы координаты векторов, не указан явно, то он предполагается ортонормированным.