Основные понятия и формулы
Прямоугольная декартова система координат на плоскости (соответственно в пространстве) состоит из фиксированной точки O – начала координат и фиксированного ортонормированного базиса  (соответственно
(соответственно  ). Прямые, проходящие через начало координат с направлением на них, задаваемым векторами
). Прямые, проходящие через начало координат с направлением на них, задаваемым векторами  и
и  называются, соответственно, осями координат
называются, соответственно, осями координат  и
и  (или
(или  и
и  ).
).
Координатами точки M в данной системе координат называются координаты радиус-вектора  в выбранном базисе:
в выбранном базисе:
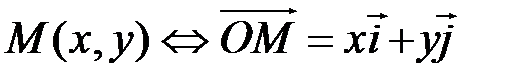
(рис. 7.1),
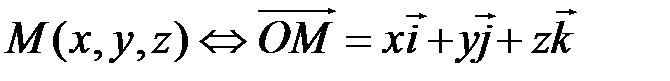
(рис.7.2).
Хотя в принятом нами определении понятие координат вектора первично, а понятие координат точки вторично, во многих задачах геометрии изначально известны только координаты точек. Если известны координаты начала
A и конца
B вектора, то
координаты вектора  находим, вычитая из координат конца B вектора соответствующие координаты его начала A:
находим, вычитая из координат конца B вектора соответствующие координаты его начала A:
 . (7.1)
. (7.1)
Координаты точки  , делящей отрезок
, делящей отрезок  ,
,  ,
,  , в отношении
, в отношении  находятся по формулам
находятся по формулам
 ,
,  ,
,  . (7.2)
. (7.2)
В частности, координаты середины M отрезка  являются полусуммами координат его концов:
являются полусуммами координат его концов:
 ,
,  ,
,  . (7.3)
. (7.3)
В случае плоскости в формулах (7.1)–(7.3) остаются только координаты  и
и  .
.

 (соответственно
(соответственно  ). Прямые, проходящие через начало координат с направлением на них, задаваемым векторами
). Прямые, проходящие через начало координат с направлением на них, задаваемым векторами  и
и  называются, соответственно, осями координат
называются, соответственно, осями координат  и
и  (или
(или  и
и  ).
). в выбранном базисе:
в выбранном базисе:
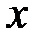



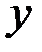


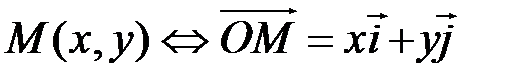 (рис. 7.1),
(рис. 7.1), 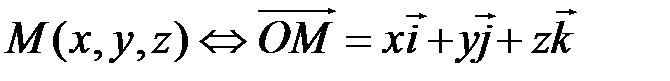 (рис.7.2).
(рис.7.2).







 находим, вычитая из координат конца B вектора соответствующие координаты его начала A:
находим, вычитая из координат конца B вектора соответствующие координаты его начала A:
 . (7.1)
. (7.1) , делящей отрезок
, делящей отрезок  ,
,  ,
,  , в отношении
, в отношении  находятся по формулам
находятся по формулам ,
,  ,
,  . (7.2)
. (7.2) являются полусуммами координат его концов:
являются полусуммами координат его концов: ,
,  ,
,  . (7.3)
. (7.3) и
и  .
.