Задачи для самостоятельного решения. В задачах 6.3.1-6.3.2дана матрица линейного оператора

В задачах 6.3.1-6.3.2дана матрица 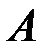линейного оператора. Записать равенство 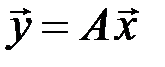в координатной форме.

6.3.1. ,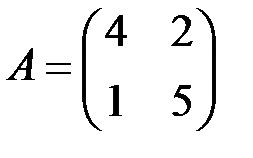

6.3.2. .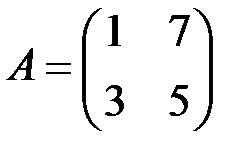

В задачах 6.3.3-6.3.6 найти вектор , в который линейный оператор 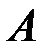преобразует вектор .

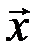6.3.3. 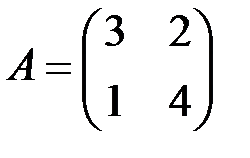, 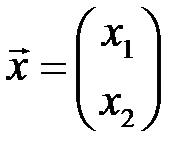.	6.3.4. , .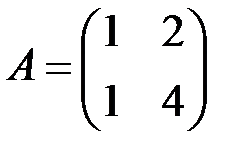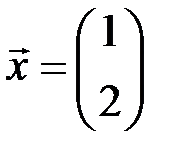
6.3.5. , 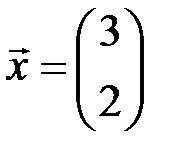.	6.3.6. , .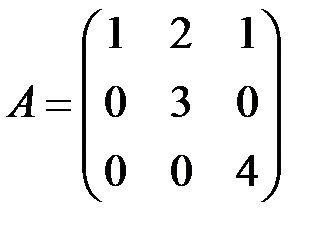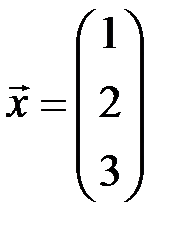

6.3.7. Найти линейный оператор (матрицу) 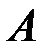, преобразующий вектор 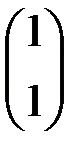в вектор 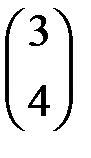, а вектор 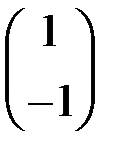в вектор .

6.3.8. Найти вектор 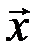, образ которого при действии линейного оператора 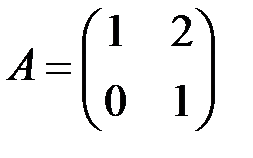– вектор .

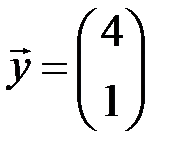Указание. Надо решить матричное уравнение относительно .

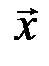6.3.9. Для линейных операторов 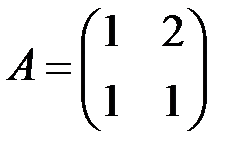и 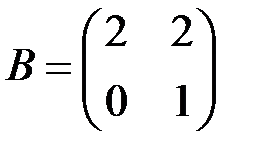найти произведение операторов 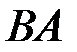, обратный оператор 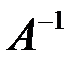и привести их координатную запись.

В задачах 6.3.10-6.3.12найти собственные значения и собственные векторы линейных операторов.

6.3.10. .

6.3.11. .

6.3.12. .