III. Теоремы остроградского-гаусса и Стокса

Теорема 8. Если функции 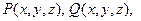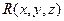непрерывно дифференцируемы в объемно односвязной области 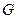, то для любой простой замкнутой области , ограниченной кусочно-гладкой поверхностью , верна формула Остроградского -Гаусса

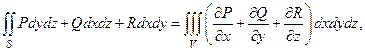(5)

где поверхностный интеграл второго рода вычисляется по внешней стороне поверхности .

Теорема 9. Пусть в некоторой пространственной области 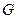, целиком содержащей кусочно-гладкую поверхность , ограниченную контуром , заданы непрерывно-дифференцируемые функции 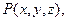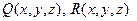. Тогда имеет место формула Стокса

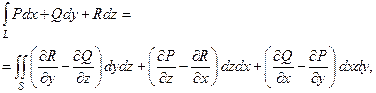(6)

где обход контура при выбранной стороне поверхности происходит в положительном направлении.

Формулу (6) иногда записывают в символическом виде

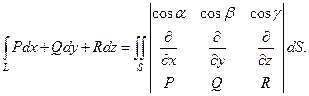(7)