Геометрические и физические приложения криволинейных интегралов первого рода

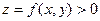Пусть во всех точках плоской кривой определена функция . Тогда площадь части цилиндрической поверхности с образующими, параллельными оси 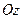и проходящими через точки кривой , ограниченной снизу дугой , сверху - линией пересечения цилиндрической поверхности с поверхностью 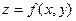, а с боков - прямыми, проходящими через точки А и В параллельно оси

Рис. 3.

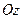(см. рис. 3), находится по формуле

.

Пусть функция 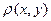, определенная на кривой , задает линейную плотность распределения массы вдоль этой кривой. Тогда справедливы следующие формулы:

а) 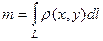- масса кривой ;

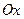б) - статические моменты кривой относительно осей и ;

в) 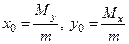- координаты центра тяжести кривой;

г) - момент инерции кривой относительно начала координат;

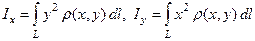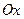д) - моменты инерции кривой относительно осей и ;

е) 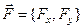- сила притяжения материальной точки массы 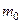материальной кривой , где

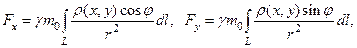
- угол между вектором и осью 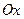, 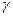- гравитационная постоянная.

Аналогичные формулы справедливы и в случае пространственной кривой.