I. Криволинейные интегралы первого рода

1.1. Определение криволинейного интеграла первого рода. Напомним, что если кривая на координатной плоскости 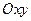задана параметрически уравнениями

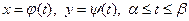, (1)

где функции 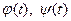непрерывны на сегменте 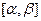, то кривая называется простой кривой. Простая кривая называется спрямляемой, если существует предел длин ломаных, вписанных в кривую, при 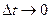(этот предел называется длиной кривой ).

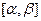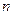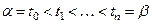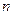Пусть - простая, спрямляемая кривая, заданная уравнениями (1), в точках которой задана функция . Разобьем сегмент на частей точками . При этом кривая разобьется на частей точками 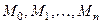. Обозначим через 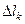длину дуги 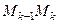, выберем на каждой дуге 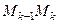некоторую точку и составим интегральную сумму

.

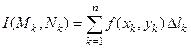Пусть .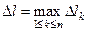

Определение. Число 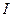называется пределом интегральных сумм при 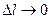, если 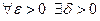такое, что для любого разбиения кривой , у которого 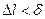, и для любого выбора точек выполняется неравенство

.

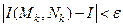Предел 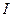интегральных сумм называется криволинейным интегралом первого рода от функции по кривой и обозначается .

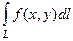Итак,

. (2)