Замена переменных в тройном интеграле

Замена переменных в тройном интеграле состоит в переходе от переменных 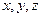к новым переменным 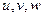по формулам

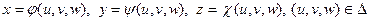. (5)

Пусть отображение (5) обладает свойствами:

I. Отображение (5) взаимно однозначно, т.е. различным точкам 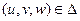соответствуют различные точки .

II. Функции 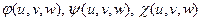имеют в области 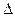непрерывные частные производные первого порядка.

III. Якобиан отображения отличен от нуля во всех точках области .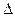

Теорема 4. Пусть и 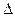- замкнутые квадрируемые области, функция ограничена в области и непрерывна всюду, кроме, быть может, некоторого множества точек объема нуль, а отображение (5) удовлетворяет условиям I-III. Тогда справедливо равенство

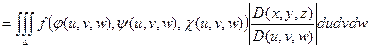(6)

Формула (6) называется формулой замены переменных в тройном интеграле. Таким образом, для замены переменных в тройном интеграле (1) необходимо в подынтегральную функцию вместо 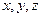подставить соответственно , а элемент объема заменить на элемент объема в криволинейных координатах .

Замену переменных используют как для упрощения подынтегральной функции, так и для упрощения области интегрирования.