Линейные уравнения

Уравнение 1-го порядка

, (5)

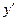линейное относительно функции и ее производной , называется линейным уравнением 1-го порядка (относительно ).

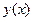Уравнение 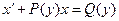- линейное относительно .

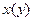Теорема 3. Если , то уравнение (5) интегрируется в квадратурах, и его единственное решение имеет вид:

.

Пример 7. Решить уравнение

.

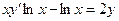Решение. Переписав данное д.у. в виде

,

убеждаемся, что это - линейное относительно 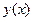д .у.

1-й способ. Применим метод вариации произвольной постоянной. Для этого найдем вначале общее решение соответствующего однородного д.у.

или .

Это д.у. с разделяющимися переменными. Разделяя переменные и интегрируя, находим его общее решение: . Проварьируем постоянную , т.е.

далее будем считать ее функцией от 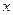. Тогда имеем:

. (6)

Найдем отсюда и подставим 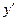в данное д.у. Тогда получим

,

откуда 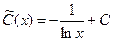или с учетом (6) окончательно находим

.

Ответ. .

2-й способ. Применим подстановку 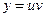, где - неизвестные функции от 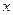. В новых переменных данное уравнение имеет вид ():

. (7)

Приравняем выражение в скобке к нулю и найдем любое частное решение уравнения

.

Это д.у. с разделяющимися переменными. Одно из его решений . С учетом найденного уравнение (7) принимает вид:

,

откуда . В итоге имеем 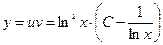или .

Ответ. .