Особые точки

Особой точкой уравнения

,

где функции P и Q непрерывно дифференцируемы, называется такая точка , в которой .

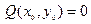Геометрический смысл особой точки заключается в том, что в ней нарушается существование или единственность решения данного дифференциального уравнения: через такую точку может не проходить ни одна из интегральных кривых уравнения, а могут проходить несколько интегральных кривых.

Для исследования особой точки уравнения

(16)

надо найти корни характеристического уравнения

. (17)

Возможны следующие случаи:

I. Корни характеристического уравнения (17) вещественные и различные:

а) . Особая точка - узел.

б) 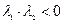. Особая точка - седло.

II. Корни характеристического уравнения (17) комплексные :

а) или . Особая точка - фокус.

б) 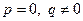. Особая точка - центр.

III. Корни кратные :

Особая точка может быть вырожденным узлом или дикритическим узлом, причем дикритический узел имеет место только в случае уравнения , а во всех остальных случаях особая точка является вырожденным узлом.

IV. Если же один или оба корня уравнения (17) равны нулю, то и, следовательно, дробь в правой части уравнения (16) сокращается. Уравнение принимает вид , и решения на плоскости изображаются параллельными прямыми.

1.7. Особые решения

Решение д.у. 1-го порядка называется особым, если в каждой его точке 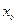из области определения нарушается свойство единственности, т.е. если через каждую точку графика , кроме этой интегральной кривой, проходит и другая интегральная кривая, имеющая в точке ту же касательную, что и решение , но не совпадающее с ним в сколь угодно малой окрестности .

Укажем несколько методов отыскания особых решений у д.у. 1-го порядка.

1.7.1. Нахождение особых решений из анализа условий

теоремы Пикара

Множество точек области D, в которых неограничена, может оказаться графиком особого решения.

1.7.2. Метод р-дискриминант

Теорема 8. Если функция является особым решением д.у. , то она удовлетворяет системе уравнений

(18)

где .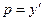

Уравнение , полученное из системы (18) исключением переменной , определяет так называемые p-дискриминантные кривые (ПДК). Из теоремы 8 следует, что каждое особое решение уравнения является ПДК. Обратное утверждение неверно. Поэтому для отыскания особых решений уравнения надо найти все его ПДК и выделить из них те, которые являются особыми интегральными кривыми.