Однородные уравнения и приводящиеся к ним

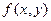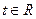Функция , определенная в области D, называется однородной функцией степени , если при любом , для которого 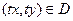, выполняется равенство

.

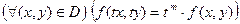Уравнение 1-го порядка 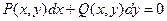, в котором 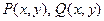- однородные функции одинаковой степени, называется однородным дифференциальным уравнением.

Уравнение 1-го порядка 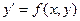называется однородным, если 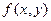- однородная функция нулевой степени.

Уравнение 1-го порядка

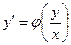(4)

называется однородным дифференциальным уравнением.

Теорема 2. Если в однородном уравнении (4) функция как функция одной переменной 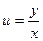непрерывна на промежутке < a;b >, причем на этом промежутке , то общее решение уравнения (1) имеет вид:

.

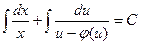Замечание 3. Если при некотором 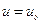окажется, что ,то функция является решением уравнения (4).

Замечание 4. На практике нет необходимости приводить однородное уравнение к виду (4), достаточно сразу сделать подстановку .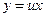

Замечание 5. Д.у.

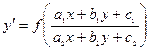, где ,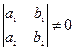

приводится к однородному уравнению заменой 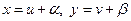, где 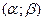- точка пересечения прямых и .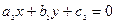

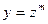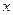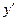Замечание 6. Некоторые уравнения можно привести к однородным заменой переменного (число обычно заранее неизвестно). Это имеет место в том случае, когда в уравнении все члены оказываются одинакового измерения, если переменному приписать измерение 1, переменному - измерение и производной - измерение .