Теорема существования и единственности решения задачи Коши

Теорема 7 (теорема Пикара). Если в уравнении функция 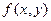непрерывна в области D и удовлетворяет в этой области условию Липшица по переменной , т.е.

то для каждой внутренней точки на достаточно малом отрезке существует единственное решение , удовлетворяющее начальному условию .

На практике вместо условия Липшица пользуются более удобным условием, достаточным для его выполнения, - условием существования и ограниченности в области D частной производной .

Для существования решения достаточно только непрерывности 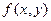в области , но при этом решение может быть не единственным.

Теорема Пеано. Пусть в уравнении функция 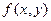непрерывна в прямоугольнике

,

причем . Тогда задача Коши на промежутке имеет по крайней мере одно решение .

Условия теоремы являются достаточными для существования единственного решения, но не необходимыми.