 |
Главная Случайная страница Контакты | Мы поможем в написании вашей работы! | |
И перпендикулярности двух плоскостей
|
|
Пусть заданы две плоскости π1 и π2:
A1 x + B1 y + C1 z + D1 = 0
A2 x + B2 y + C2 z + D2 = 0.
Угол φ между двумя плоскостями π1 и π2 определяется углом между нормальными векторами 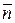 1 = (А1,В1,С1) и
1 = (А1,В1,С1) и 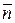 2 = (А2,В2,С2) плоскостей π1 и π2. Поэтому
2 = (А2,В2,С2) плоскостей π1 и π2. Поэтому  или
или
 . (3.24)
. (3.24)
Для определения острого угла между двумя плоскостями следует взять модуль правой части.
Если плоскости π1 и π2 перпендикулярно, то перпендикулярны и нормальные векторы 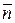 1 и
1 и 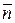 2, т.е.
2, т.е. 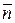 1 ∙
1 ∙ 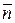 2 = 0 или
2 = 0 или
А1 А2 + B1 B2 + C1 C2 = 0. (3.25)
Полученное равенство (3.25) и есть условие перпендикулярности двух плоскостей.
Если плоскости π1 и π2 параллельны, то параллельны и нормальные векторы 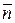 1 и
1 и 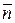 2, т.е.
2, т.е. 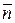 1 = λ
1 = λ 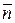 2 или
2 или
 . (3.26)
. (3.26)
Это и есть условие параллельности двух плоскостей π1 и π2.
Дата публикования: 2015-07-22; Прочитано: 199 | Нарушение авторского права страницы | Мы поможем в написании вашей работы!
