Деление отрезка в данном отношении

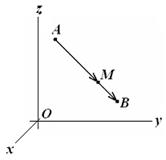Требуется разделить отрезок АВ, соединяющий точки А(х₁,у₁,z₁) и В(х₂,у₂,z₂) в заданном отношении λ>0, т.е. найти координаты точки М (х,у,z) отрезка АВ такой, что АМ/МВ = λ (см. рис. 3.10).

Решение. Введём в рассмотрение векторы АМ и МВ. Точка М делит отрезок АВ в отношении λ если АМ = = λ МВ. Но АМ = (х – х₁, у – у₁, z – z₁) и МВ = (х₂ – х, у₂ – у, z₂ - z), поэтому

(х – х₁) = λ(х₂ – х), (y – y₁) = λ(y₂ – y) и (z – z₁) = λ(z₂ – z) Рис. 3.10.

или 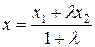, . . (3.19)

Формулы (3.19) называются формулами деления отрезка в данном отношении. В частности, при λ = 1, т.е. если АМ = МВ, то они примут вид

, , .

В этом случае точка М (х, у, z) является серединой отрезка АВ.

Замечание. Если λ < 0, то точка М лежит вне отрезка АВ – говоря, что точка М делит отрезок АВ внешним образом.