Уравнение плоскости, проходящей через три данные точки

Три точки пространства, не лежащие на одной прямой, определяют единственную плоскость. Найдём уравнение плоскости π, проходящей через три данные точки М₁ (х₁,у₁,z₁), М₂ (х₂,у₂,z₂), и М₃ (х₃,у₃,z₃), не лежащие на одной прямой.

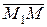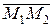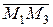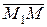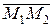
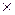
Возьмём на плоскости произвольную точку М (х,у,z) и образуем векторы = (х – х₁, y – y₁, z – z₁), = (х₂ – х₁, y₂ – y₁, z₂ – z₁), = (х₃ – х₁, y₃ – y₁, z₃ – z₁). Эти векторы лежат на плоскости π, следовательно, они компланарны. Используем условие компланарности трёх векторов (их смешанное произведение равно нулю), получим ∙( 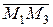) = 0, т.е.

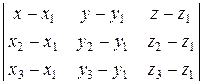= 0. (3.22)

Уравнение (3.22) есть уравнение плоскости, проходящей через три точки.