Общее уравнение плоскости

Рассмотрим общее уравнение первой степени с тремя переменными х,у и z:

A x + B y + C z + D = 0. (3.21)

Полагая, что по крайней мере один из коэффициентов А, В или С не равен нулю, например В ≠ 0, перепишем уравнение (3.21) в виде

A (x - 0) + B (y + D/B) + C (z - 0) = 0.

Сравнивая данное уравнение с уравнением (3.20), видим, что это уравнение является уравнением плоскости с нормальным вектором 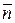= (А,В,С), проходящей через точку М₁ (0, - (D/B), 0).

Итак, уравнение (3.21) определяет в системе координат Охyz некоторую плоскость. Уравнение (3.21) называется общим уравнением плоскости.