Несобственные интегралы. 1. Вычислить несобственный интеграл

Вычисление интегралов с бесконечными пределами от непрерывных функций.

1. Вычислить несобственный интеграл

Решение. Подынтегральная функция определена и непрерывна при всех значениях х и, следовательно, имеет первообразную Ф(х)= По определению имеем:

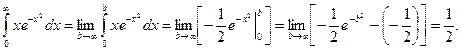
2. Вычислить несобственный интеграл

Решение. В этом примере оба предела интегрирования бесконечны: поэтому предварительно разбиваем данный интеграл на два:

3. Сходится ли несобственный интеграл

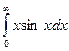
Решение.

Применим правило интегрирования по частям, полагая 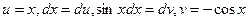. Будем иметь:

Этот предел не существует, следовательно, интеграл расходится.

4. Вычислить интеграл.

Решение. Положив , получим:

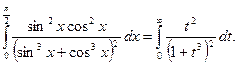
Мы получили несобственный интеграл. Он легко вычисляется следующим образом:

Вычисление несобственных интегралов от неограниченных функций.

1. Вычислить несобственный интеграл.

Решение. Преобразуем интеграл следующим образом:

В интеграле I₁ подынтегральная функция непрерывна в промежутке [1;2], поэтому его можно вычислить по формуле Лейбница

.

Интеграл I₂ несобственный, так как подынтегральная функция при . По определению имеем:

Окончательно,

2. Вычислить несобственный интеграл

.

Решение. Преобразуем данный интеграл следующим образом:

.

Интеграл I₁ легко вычисляется при помощи формулы Ньютона-Лейбница (законность применения формулы Ньютона-Лейбница вытекает из непрерывности подынтегральной функции) . Интеграл I₂ является несобственным интегралом.

Несобственный интеграл I₂ следует представить в виде суммы двух интегралов (ибо точка разрыва х=0 лежит внутри промежутка интегрирования):

Итак, .

3. Вычислить несобственный интеграл

.

Решение. Подынтегральная функция неограниченна в окрестностях точек х=0 и х=1. Поэтому представим интеграл в виде суммы двух интегралов:

.

Оба интеграла I₁ и I₂ несобственные.

По определению имеем:

4. Вычислить несобственный интеграл

.

Решение. Здесь подынтегральная функция терпит бесконечный разрыв в точке х=1, но ее первообразная непрерывна на промежутке [1;2]. Поэтому здесь применима формула Ньютона-Лейбница.

.

Вариант 1

1.Найти интегралы: 1) 2) 3) 4)

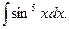
2. Установите, будет ли сходиться несобственный интеграл. В случае сходимости найдите его значение.

3. Вычислите площадь эллипса: , где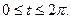

4. Вычислите площадь области, ограниченной осью ОХ и графиком функции:

5. Найдите длину дуги кривой:

6. Вычислите площадь боковой поверхности конуса с высотой h и радиусом основания r.

Вариант 2

1.Найдите интегралы: 1) 2) 3)

4)

2. Установите, будет ли сходиться несобственный интеграл . В случае сходимости найдите его значение.

3. Найдите площадь области, ограниченной кардиоидой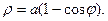

4. Найдите площадь области, ограниченной кривыми:

5. Вычислите длину дуги кривой: , заключенной между точками пересечения с осью ОХ.

6. Вычислите объем тела, образованного вращением вокруг оси ОХ криволинейной трапеции, ограниченной

Вариант 3

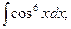1. Найдите интегралы: 1) 2) 3) 4)

2. Установите, будет ли сходиться несобственный интеграл. В случае сходимости найдите его значение.

3. Найдите площадь области, ограниченной кривой и осью ОХ.

4. Найдите площадь области, ограниченной линией , и осью ОХ.

5. Вычислить длину дуги окружности

6. Найти объем тела, полученного от вращения фигуры, ограниченной линиями вокруг оси ОХ.

Вариант 4

1. Найдите интегралы: 1) 2) 3) 4)

2. Установите, будет ли сходиться несобственный интеграл. В случае сходимости найдите его значение.

3. Найдите площадь области, ограниченной астроидой

.

4. Найдите площадь области, ограниченной осями ОХ, ОУ и графиком функции

5. Найдите длину дуги кривой между точками с абсциссами х=0 и х= .

6. Найти площадь поверхности, полученной вращением кардиоиды вокруг полярной оси.

Вариант 5

1. Найдите интегралы: 1) 2) 3) 4)

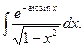
2. Установите, будет ли сходиться несобственный интеграл. В случае сходимости найдите его значение.

3. Найдите площадь области, ограниченной лемнискатой

4. Найдите площадь области, ограниченной графиком функции и осью ОХ.

5. Найдите длину дуги кривой

,

6. Найти объем тела, полученного от вращения вокруг оси ОХ фигуры, ограниченной линиями: .

Вариант 6

1. Найдите интегралы: 1) 2) 3) 4)

2. Установите, будет ли сходиться несобственный интеграл. В случае сходимости найдите его значение.

3. Найдите площадь области, ограниченной кардиоидой

.

4. Найдите площадь области, ограниченной графиком функции , осью ОХ и прямой х=а, где а – точка экстремума этой функции.

5. Найдите длину дуги кривой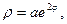

6. Найти площадь поверхности эллипсоида, полученного от вращения эллипса вокруг оси ОУ.

Вариант 7

1. Найдите интегралы: 1) 2) 3) 4)

2. Установите, будет ли сходиться несобственный интеграл. В случае сходимости найдите его значение.

3. Найдите площадь области, ограниченной кривыми

4. Найдите площадь области, ограниченной кривой и осью абсцисс.

5. Найдите длину дуги кривой , заключенной внутри параболы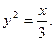

6. Найти объем тела, полученного вращением вокруг оси ОХ фигуры, ограниченной циклоидой , и осью ОХ.

Вариант 8

1. Найдите интегралы: 1) 2) 3) 4)

2. Установите, будет ли сходиться несобственный интеграл. В случае сходимости найдите его значение.

3. Найдите площадь области, ограниченной кривой .

4. Найдите площадь области, ограниченной осью ОХ и кривой .

5. Найдите длину дуги кривой между точками с абсциссами х=1 и х=2

6. Найти площадь поверхности, образованной вращением петли кривой вокруг оси ОХ.

Вариант 9

1. Найдите интегралы: 1) 2) 3) 4)

2. Установите, будет ли сходиться несобственный интеграл. В случае сходимости найдите его значение.

3. Найдите площадь области, ограниченной кривой .

4. Найдите площадь области, ограниченной осью ОХ и кривой .

5. Найдите длину дуги кривой , отсеченной прямой х=4/3.

6. Найти площадь поверхности шаровой чаши, полученной от вращения круга вокруг оси ОХ в пределах от 0 до 1.

Вариант 10

1. Найдите интегралы: 1) 2) 3) 4)

2. Установите, будет ли сходиться несобственный интеграл. В случае сходимости найдите его значение.

3. Найдите площадь области, ограниченной петлей кривой .

4. Найдите площадь области, ограниченной улиткой Паскаля .

5. Найдите длину дуги кривой

, .

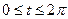6. Круг радиуса 2 с центром в точке (0,7) вращается вокруг оси ОХ. Найти объем полученного тела вращения.

ОГЛАВЛЕНИЕ

План чтения лекций……………………...……………………………………….3

§1. Неопределенный интеграл……………................................................….......4

1. Первообразная функция. Неопределенный интеграл................................4

2. Основные свойства неопределенного интеграла.....................…...…….....6

3. Метод непосредственного интегрирования и подстановки....……….........9

4. Способы интегрирования дробей вида ...............…………….........11

5. Интегрирование по частям........…………………………………………....16

§2. Определенный интеграл.......................................................................17

1. Понятие об определенном интеграле……………………………..............17

2. Определенный интеграл с переменным верхним пределом……………...18

3. Основные свойства определенного интеграла............................……..…20

4. Теорема о среднем.......................................................................................22

5. Интегрирование по частям в определенном интеграле.............................23

6. Замена переменной в определенном интеграле.........................................24

7. Несобственные интегралы..............................................................................25

§3. Приложения определенного интеграла......................................................26

1. Применение определенного интеграла к вычислению площадей плоских фигур и длинны дуги....................................................................................26

2. Вычисление объема тела.............................................................................31

3. Вычисление площади поверхности тела вращения....................................33

§4. Понятие о приближенном вычислении определенных интегралов........34

1. Метод трапеций...........................................................................................34

2. Формула Симпсона....................................................................................36

КОНТРОЛЬНАЯ РАБОТА............................................................................38