 |
Главная Случайная страница Контакты | Мы поможем в написании вашей работы! | |
Вычисление длины дуги плоской кривой
|
|
1. Вычислить длину дуги  цепной линии, заданной уравнением
цепной линии, заданной уравнением
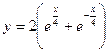 ,
,
от точки х=0 до точки х=4.
Решение. Воспользуемся формулой 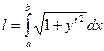 . Имеем:
. Имеем:
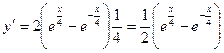
и
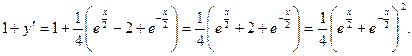
Отсюда
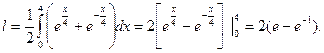
2. Вычислить длину дуги кривой:
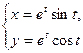
от t=0 до t= 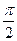 .
.
Решение. Дифференцируя по t параметрические уравнения кривой, получим:
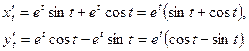
Пользуясь формулой для длины дуги в параметрическом виде, получим:
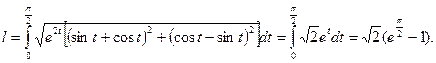
3. Вычислить длину дуги кривой, заданной параметрически
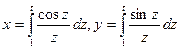
от начала координат (t=1) до ближайшей точки с вертикальной касательной.
Решение. Очевидно, что при t=1кривая проходит через начало координат. Далее,
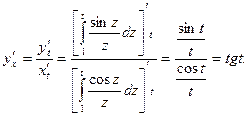
Таким образом, касательная к данной кривой будет вертикальна во всех точках, для которых cost=0, т.е. в точках 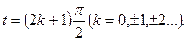 Ближайшей к началу координат (t=1) является точка со значением параметра
Ближайшей к началу координат (t=1) является точка со значением параметра 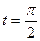 .
.
Таким образом, пределы интегрирования найдены: 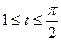 . Теперь
. Теперь
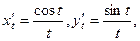
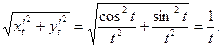
Следовательно,
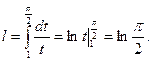
4. Найти длину замкнутой кривой 
Решение. Так как должно быть 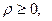 то
то 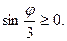 Отсюда
Отсюда 
 При изменении φ от 0 до
При изменении φ от 0 до 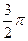 длина радиус-вектора ρ возрастает от 0 до а, а конец радиус-вектора описывает дугу OAMB (рис.1). Затем при изменении φ от
длина радиус-вектора ρ возрастает от 0 до а, а конец радиус-вектора описывает дугу OAMB (рис.1). Затем при изменении φ от 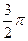 до 3π величина ρ убывает от а до 0; при этом описывается дуга BCAO, симметричная дуге OAMB относительно прямой
до 3π величина ρ убывает от а до 0; при этом описывается дуга BCAO, симметричная дуге OAMB относительно прямой 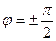 .
.
Теперь вычислим длину кривой.
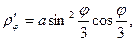
|
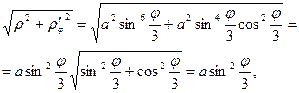
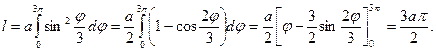
Дата публикования: 2015-07-22; Прочитано: 964 | Нарушение авторского права страницы | Мы поможем в написании вашей работы!
