Метод трапеций

Определенный интеграл

(1)

от заданной непрерывной функции y=f(x) точно вычисляется далеко не всегда. Однако, пользуясь его геометрическим смыслом, можно дать ряд приближенных формул, с помощью которых этот интеграл находится с любой степенью точности. Мы здесь рассмотрим простейшую из них, так называемую формулу трапеций.

Как известно, интеграл (1) представляет собой площадь криволинейной трапеции, ограниченной линией y=f(x), осью Ох и двумя ординатами х=а и х=b (рис. 12). Разобьем отрезок [a,b] на n равных частей длины 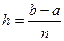(шаг разбиения).

Пусть х₀, х₁, …, х_n (x₀=a, x_n=b) – абсциссы точек деления и у₀, у₁, …, у_n – соответствующие ординаты кривой. Имеем расчетные формулы

Х_i= х₀ + ih, y_i=f(x_i)

(i=0, 1, 2, …, n). В результате построения наша криволинейная трапеция разбилась на ряд вертикальных полосок одной и той же ширины h, каждую из которых приближенно примем за трапецию. Суммируя площади этих трапеций, будем иметь

или

(2)

(формула трапеций). Формулу (2) можно коротко записать в виде

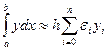, (3)

Где 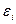=1/2 при i=0 и i=n и 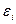=1 при i=1, 2, …, n-1.

Погрешность

называется остаточным членом формулы трапеций (3). Доказано, что если функция y=f(x) имеет непрерывную вторую производную 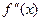на отрезке [a,b], то где

Пример. Приближенно вычислить .

Разобьем промежуток интегрирования [0, 1] на 10 частей (n=10); следовательно, шаг h=0,1.

i	xi	εiyi
	0,0 0,1 0,2 0,3 0,4 0,5 0,6 0,7 0,8 0,9 1,0	0,5000* 1,0050 1,0198 1,0440 1,0770 1,1180 1,1662 1,2207 1,2806 1,3454 0,7071*
∑	11,4838

Абсциссы точек деления x_i(i=0, 1, …, 10) и соответствующие им ординаты , вычисленные с помощью таблицы квадратных корней, приведенных в таблице, причем ординаты для удобства умножены на множитель ε_i такой, что ε_i=1/2 при i=0, i=10 (отмечены звездочкой) и ε_i=1 пр и i=1, 2, …, 9.

По формуле (3) имеем I≈0.1*11.4838≈1.148. Точное значение интеграла равно I= .