Вычисление площадей фигур

1. Вычислить площадь фигуры, ограниченной прямой у=х и параболой у=2-х².

Решение. Найдем абсциссы точек пересечения прямой с параболой, решив систему уравнений (рис.2).

Решая систему, получим х1=-2, х2=1 – это и будет пределы интегрирования. Искомая площадь равна:

2. Вычислить площадь сегмента круга с основанием а и высотой h. Радиус круга равен r.

Решение: Расположим оси координат так, как показано на рис. 3 Площадь S криволинейной трапеции ABCDE равна.

.

Из рис. 3 видно, что , а , где α- центральный угол, опирающийся на основание сегмента. Следовательно, . Чтобы получить искомую площадь сегмента, надо из площади криволинейной трапеции ABCDE вычесть площадь прямоугольника ABDE.

Таким образом,

Легко заметить, что

.

Подставив, получим:

.

Эта формула хорошо известна из элементарной математики и может быть получена геометрическим путем.

3. Найти площадь фигуры, ограниченной двумя ветвями кривой

(у-х)²=х³ и прямой х=1.

Решение. Заметим, что у как неявная функция от х, определена лишь при х≥0 (левая часть уравнения всегда неотрицательна). Найдем уравнение двух ветвей кривой:

Очевидно, что при х≥0 (рис. 4).

Поэтому

Замечание. При вычислении площади криволинейной трапеции в случае, когда верхняя граница задана параметрическими уравнениями , , в формуле надо сделать замену переменной. Положив . Тогда получим:

Рис.4

Где α и β – значения параметра t, соответствующие значениям х=а и х=b, т.е. .

4. Найти площадь фигуры, ограниченной одной аркой циклоиды

и осью Ох.

Решение. Арка циклоиды описывается при изменении t в пределах от 0 до 2π, так как у(0)=у(2π)=0, а в остальных точках указанного промежутка у>0. Пределы интегрирования равны соответственно х(0)=0 и х(2π)=2πа.

Следовательно, искомая площадь равна:

.

Сделаем подстановку x=a(t-sint), y=a(1-cost), dx=a(1-cost)dt. Когда х пробегает отрезок [0;2πa], t пробегает отрезок [0;2π]. Поэтому

Так как площадь круга радиуса а равна , то полученный результат показывает, что площадь арки циклоиды в три раза больше площади круга.

5. Найти площадь фигуры, ограниченной полярной осью и первым витком спирали Архимеда

.

Решение

.

Заметим, что точка С пересечения первого витка спирали с полярной осью отдалена от полюса на расстояние . Поэтому круг радиуса ОС имеет площадь .

Таким образом, площадь фигуры, ограниченной полярной осью и первым витком спирали Архимеда, равна 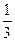площади круга с радиусом, равным наибольшему из радиус-векторов точек витка (рис. 5). К этому выводу пришел еще Архимед.

	Рис.5		Рис. 6

6. Найти площадь фигуры, ограниченной одним лепестком кривой (лемниската).

Решение. Правая часть уравнения кривой неотрицательна при значениях φ, для которых 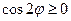. Поэтому первый лепесток лежит в углу, где , т.е. . Следовательно (рис. 6),

.