Вычисление объема тела

Определение: тело Т называется регулярным, если существует такая плоскость π, что

а) тело Т лежит по одну сторону от нее;

б) все сечения тела плоскостями, параллельными плоскостями, квадрируемы;

в) площадь S сечения Q, параллельного плоскости π и отстоящего от нее на расстояние х, является непрерывной функцией от х: S=S(x);

г) если S(x₁)≤S(x₂), то проекция сечения Q(x₂) на плоскость π содержит проекцию сечения Q(x₁) на ту же плоскость.

Теорема: Если тело Т регулярно, то оно кубируемо, причем его объем выражается формулой

Пример: Найти объем пирамиды, площадь основания которой равна S, а высота равна Н.

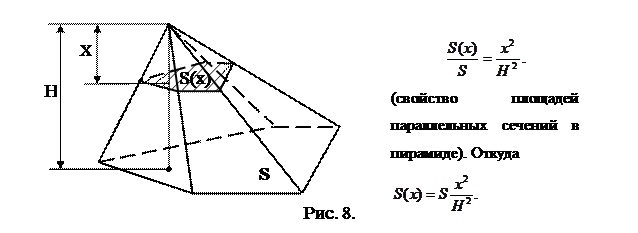
Если Т – тело вращения, полученное от вращения вокруг ОХ криволинейной трапеции, ограниченной прямыми х=а; х=b; у=0 и у=f(x), то это тело регулярно, причем и

Пример: Найти объем прямого кругового конуса, радиус основания которого R, высота Н. Этот конус получается от вращения треугольника ОАН вокруг оси ОХ (рис.9).

Замечание: Если кривая f(x) задана параметрически или в полярной системе координат, то в определенном интеграле надо сделать замену переменных. Не забудьте про новые пределы интегрирования.

Пример: Найти объем эллипсоида вращения, полученного от вращения эллипса вокруг оси ОХ (рис. 10).