Теорема. Для того, чтобы существовал базис, в котором матрица оператора является диагональной, необходимо и достаточно

Для того, чтобы существовал базис, в котором матрица оператора является диагональной, необходимо и достаточно, чтобы размерности подпространств собственных векторов были равны кратностям соответствующих собственных значений как корней характеристического многочлена оператора .

Задача. Можно ли матрицу А линейного оператора линейного пространства V(P) привести к диагональному виду путем перехода к новому базису? Если можно, то найти этот базис и соответствующую ему матрицу.

а) б)

с) d)

Решение. Для каждой матрицы найдем характеристический многочлен

а) b)

c) d)

В случае а) не все корни многочлена действительны и, следовательно, матрица А не подобна диагональной матрице с действительными элементами.

В случае b) корнями многочлена являются различные действительные числа оператор с простым спектром, его матрица приводится к диагональному виду:

(по диагонали расположены собственные значения оператора ) в базисе где — собственный вектор, принадлежащий собственному значению

Найдем такие векторы.

Общее решение:

фундаментальная система решений:

х 1	х2	х 3
(0		0) = а i

Множество собственных векторов для — это \ .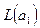

.

Общее решение:

фундаментальная система решений:

х 1	х 2	х 3
(-2		-3)= а 2

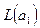\ — это множество собственных векторов для .

Общее решение:

Фундаментальная система решений

х 1	х 2	х 3
(-2		0)= а 3

\ — это множество собственных векторов для

Векторы образуют базис в котором оператор имеет матрицу

В случаях с) и d) по виду многочлена нельзя сказать, будет ли матрица подобна диагональной, так как имеются кратные корни. В этих случаях необходимо выяснить, сколько линейно независимых собственных векторов имеет собственное значение, являющееся кратным корнем многочлена

с). — двукратный корень. Найдем для него множество собственных векторов из условия

Общее решение:

Размерность пространства решений этой системы равна n-r (п — числонеизвестных,

r — ранг матрицы системы), то есть 3 - 1 = 2 — совпадает с кратностью собственного значения. Фундаментальная система решений:

х 1	х 2	х 3
(1 (0		2) = а 1 0) = а 2

а ₁, а ₂ - линейно независимы. Множество собственных векторов L(a₁,a₂)\ .

В этом случае матрица может быть приведена к диагональному виду

в базисе а ₁, а ₂, а ₃, где а ₁, а ₂ — найденные векторы, а ₃ — собственный вектор, принадлежащий простому собственному значению Его найдем из системы:

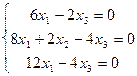Общее решение: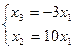

Фундаментальная система решений:

х 1	х 2	х 3
(1		-3) = а 3

\ — множество собственных векторов для

d). - двукратный корень многочлена Найдем для него множество собственных векторов из условия

Общее решение: .

Размерность пространства решений этой системы равна 3 – 2 = 1, не совпадает с кратностью собственного значения в этом случае матрица А не может быть приведена к диагональному виду путем перехода к новому базису.

ЛИТЕРАТУРА

1. Мальцев А.И. Основы линейной алгебры. — М.: Наука, 1975
2. Курош А.Г. Курс высшей алгебры. — М.: Наука, 1975
3. Куликов Л.Я. Алгебра и теория чисел. — М.: Высшая школа, 1979
4. Проскуряков И.В. Сборник задач по линейной алгебре. — М.: Наука, 1984