 |
Главная Случайная страница Контакты | Мы поможем в написании вашей работы! | |
Доказательство. Пусть оператор обратимый, обозначим
|
|
 Пусть оператор
Пусть оператор  обратимый, обозначим
обратимый, обозначим 

Докажем, что  инъективно, то есть для любых
инъективно, то есть для любых  если
если  то
то 
Действительно, если  то
то  или
или  или
или  то есть
то есть 
Отображение  сюрьективно.
сюрьективно.
Действительно, для любого 
 то есть
то есть  — это прообраз для а при отображении
— это прообраз для а при отображении  . Таким образом,
. Таким образом,  — биекция.
— биекция.
 Пусть
Пусть  — инъективное отображение, тогда
— инъективное отображение, тогда  имеет единственный
имеет единственный
прообраз при отображении  , то есть
, то есть 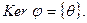
 Если
Если  то
то 
 Пусть
Пусть  Известно, что
Известно, что  , тогда
, тогда 
 Пусть
Пусть  Так как
Так как 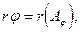 то
то  то есть ранг матрицы равен ее порядку, значит матрица
то есть ранг матрицы равен ее порядку, значит матрица  обратима.
обратима.
 — матрица оператора
— матрица оператора  в некотором базисе
в некотором базисе 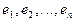 .
.
 . Пусть
. Пусть  обратима, то есть существует матрица B, такая, что
обратима, то есть существует матрица B, такая, что
 . В является матрицей некоторого оператора
. В является матрицей некоторого оператора 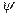 в том же базисе
в том же базисе 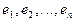 , то есть
, то есть  Тогда
Тогда  .
.
 — матрица оператора
— матрица оператора  в базисе
в базисе 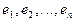 .
.
 — матрица оператора
— матрица оператора  в базисе
в базисе 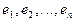 .
.
Из условия  получаем
получаем  отсюда
отсюда  то есть
то есть 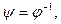 оператор
оператор  является обратимым.
является обратимым.
Дата публикования: 2015-07-22; Прочитано: 232 | Нарушение авторского права страницы | Мы поможем в написании вашей работы!
