Доказательство. По определению собственные векторы являются ненулевыми, поэтому теорема верна

Индукция по m.

По определению собственные векторы являются ненулевыми, поэтому теорема верна

для m = 1.

Предположим, что теорема верна для любой системы из m- 1 собственных векторов.

Докажем, что теорема верна для m векторов.

Составим уравнение:

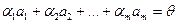(1)

Подействуем на обе части (1) оператором , так как — линейный оператор, то получим

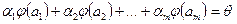(2)

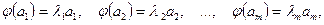
(2) принимает вид:

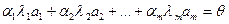(3)

Умножим (1) на 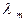и вычтем из (3):

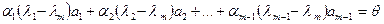(4)

По предположению векторы 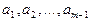линейно независимы, поэтому слева в (4) — тривиальная линейная комбинация, то есть

Так как собственные значения попарно различны, то из последних равенств следует, что 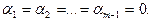Тогда (2) принимает вид: но 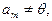значит 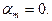Таким образом, слева в (1) 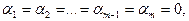векторы 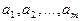линейно независимы. Что требовалось доказать.

Следствие: Любой линейный оператор, действующий в n-мерном векторном пространстве, не может иметь больше n попарно различных собственных значений.