 |
Главная Случайная страница Контакты | Мы поможем в написании вашей работы! | |
Доказательство. С заданием координатного базиса устанавливается взаимно однозначное соответствие между множеством линейных операторов пространства V(P) и множеством
|
|
С заданием координатного базиса 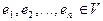 устанавливается взаимно однозначное соответствие между множеством линейных операторов пространства V(P) и множеством квадратных матриц n- ного порядка над Р:
устанавливается взаимно однозначное соответствие между множеством линейных операторов пространства V(P) и множеством квадратных матриц n- ного порядка над Р:

Оно сохраняет все главные операции алгебры 



Следовательно, рассматриваемое отображение Q(P) на множество квадратных матриц n -ного порядка над Р является изоморфизмом, а соответствующие алгебры изоморфны.
Задача. 

Линейный оператор  пространства
пространства  переводит векторы
переводит векторы  в векторы
в векторы  соответственно, оператор
соответственно, оператор  переводит векторы
переводит векторы  в векторы
в векторы  соответственно. Найти матрицы операторов
соответственно. Найти матрицы операторов  и
и  в базисах
в базисах  и
и  используя матрицы перехода от одного базиса к другому.
используя матрицы перехода от одного базиса к другому.
Решение. Найдем матрицу оператора  в базисе
в базисе  Для этого найдем координаты векторов
Для этого найдем координаты векторов  в базисе
в базисе 

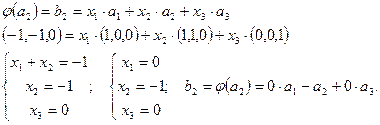


 — матрица оператора
— матрица оператора  в базисе
в базисе 
Аналогично найдем матрицу оператора 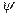 в базисе
в базисе  для этого нам понадобятся координаты
для этого нам понадобятся координаты  в базисе
в базисе 

Системы для  будут отличаться от последней системы линейных уравнений только столбцом свободных членов. Поэтому будем решать сразу три системы.
будут отличаться от последней системы линейных уравнений только столбцом свободных членов. Поэтому будем решать сразу три системы.




 — это матрица оператора
— это матрица оператора 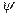 в базисе
в базисе  .
.
Матрица суммы операторов  в базисе
в базисе  :
:

Составим матрицу перехода от базиса  к базису
к базису  Для этого выразим
Для этого выразим  через
через  Мы делали это выше. Координаты
Мы делали это выше. Координаты  располагаем в столбцы матрицы перехода с теми же номерами.
располагаем в столбцы матрицы перехода с теми же номерами.

Обозначим  и
и  матрицы операторов
матрицы операторов  и
и  в базисе
в базисе 
Запишем формулы связи между матрицами оператора в различных базисах:

Найдем 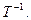




Дата публикования: 2015-07-22; Прочитано: 315 | Нарушение авторского права страницы | Мы поможем в написании вашей работы!
