 |
Главная Случайная страница Контакты | Мы поможем в написании вашей работы! | |
Определение. Квадратные матрицы А и В n-ного порядка называются подобными, если существует обратимая матрица С, такая
|
|
Квадратные матрицы А и В n-ного порядка называются подобными, если существует обратимая матрица С, такая, что

Нетрудно проверить, что отношение подобия на множестве всех квадратных матриц n -ного порядка является эквивалентностью.
Из теоремы (1) следует, что матрицы линейного оператора ненулевого конечномерного векторного пространства относительно любых двух базисов пространства подобны.
Задача. Линейный оператор 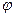 в базисе
в базисе  имеет матрицу
имеет матрицу
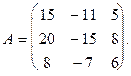 Найти матрицу оператора
Найти матрицу оператора  в базисе
в базисе

Решение. Пусть  — базис (7),
— базис (7),  — базис (8). Составим матрицу перехода от (7) к (8), располагая координаты
— базис (8). Составим матрицу перехода от (7) к (8), располагая координаты  относительно базиса (7) в i- тый столбец матрицы:
относительно базиса (7) в i- тый столбец матрицы:

Пусть В — матрица оператора  в базисе (8),
в базисе (8),  Найдем
Найдем  .
.




= 

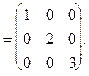
Дата публикования: 2015-07-22; Прочитано: 254 | Нарушение авторского права страницы | Мы поможем в написании вашей работы!
