 |
Главная Случайная страница Контакты | Мы поможем в написании вашей работы! | |
Доказательство. — матрица оператора в некотором координатном базисе
|
|
Пусть  где
где
 —
—
— матрица оператора 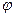 в некотором координатном базисе
в некотором координатном базисе  . Возьмем любой
. Возьмем любой  .
.
Пусть 
Запишем формулу связи между координатами х и  :
:
 .
.
Это матричное уравнение запишем в виде системы
 (1)
(1)
Видим, что  тогда и только тогда, когда его координаты удовлетворяют системе (1). Следовательно,
тогда и только тогда, когда его координаты удовлетворяют системе (1). Следовательно,  совпадает с пространством решений системы (1), поэтому
совпадает с пространством решений системы (1), поэтому  где
где 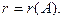 Получаем, что
Получаем, что 
Задача. Линейный оператор 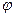 пространства
пространства  в базисе
в базисе  задан матрицей
задан матрицей  . Найти образ вектора
. Найти образ вектора  . Найти ядро, дефект, область значений и ранг
. Найти ядро, дефект, область значений и ранг 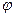 .
.
Дата публикования: 2015-07-22; Прочитано: 288 | Нарушение авторского права страницы | Мы поможем в написании вашей работы!
