 |
Главная Случайная страница Контакты | Мы поможем в написании вашей работы! | |
Доказательство. Полагая получим из (3) равенство первых столбцов матриц А и В
|
|
Полагая 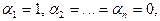 получим из (3) равенство первых столбцов матриц А и В.
получим из (3) равенство первых столбцов матриц А и В.
Полагая 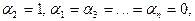 получим равенство вторых столбцов матриц А и В. и т.д.
получим равенство вторых столбцов матриц А и В. и т.д.
Вернемся к координатным базисам (1) и (2). Можно векторы системы (1) выразить через базис (2).
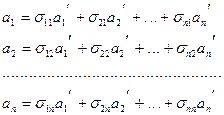
Матрица 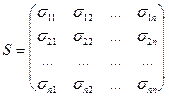 является матрицей перехода от базиса (2) к базису (1).
является матрицей перехода от базиса (2) к базису (1).
Пусть 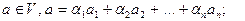
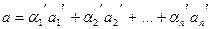
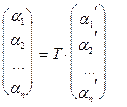 (4),
(4), 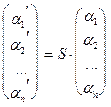 (5)
(5)
Подставим (5) в (4):
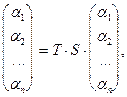 отсюда по лемме
отсюда по лемме 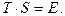
Подставим (4) в (5):
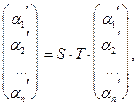 по лемме отсюда следует, что
по лемме отсюда следует, что 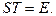
Таким образом, 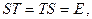 матрица перехода от одного базиса к другому всегда имеет обратную, которая является матрицей обратного перехода:
матрица перехода от одного базиса к другому всегда имеет обратную, которая является матрицей обратного перехода: 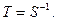
Дата публикования: 2015-07-22; Прочитано: 211 | Нарушение авторского права страницы | Мы поможем в написании вашей работы!
