Биномиальное распределение (распределение Бернулли)

Проводим n независимых испытаний, в каждом из которых событие А может произойти («успех») или не произойти («неудача»). Вероятность успеха (так же, как и неудачи) не изменяется от испытания к испытанию. В таком случае говорят, что имеет место схема испытаний Бернулли. Пусть p – вероятность успеха, а q=1-p – вероятность неудачи. Тогда вероятность того, что при n испытаниях событие А осуществится ровно k раз (и не осуществится n-k раз), выражается по формуле Бернулли: P_n(k)=C_n^kp^kq ^n-k, где C_n^k – число сочетаний из n по k.

Биномиальное распределение [3] (распределение Бернулли) – распределение дискретной случайной величины, принимающей целочисленные значения k=0, 1, 2,…, n с вероятностями P_n(k)=C_n^kp^k(1-p) ^n-k.

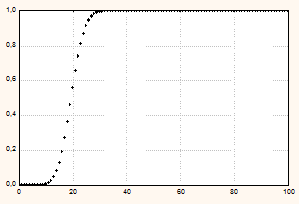
Если СВ X имеет биномиальное распределение то ее математическое ожидание М X=np, а дисперсия D X = np(1-p). Графики функции распределения Бернулли для p=0,1 и p=0,2, n=30 и n=100 см. на рис. 5.7.

n=30, p=0,1	n=100, p=0,1
n=30, p=0,2	n=100, p=0,2

Рис. 5.7.