Нормальный закон распределения. Нормальный закон распределения наиболее часто встречается на практике

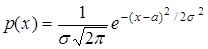Если X – СВ, имеющая нормальное распределение с параметрами a и s, то М X = a и D X=s².

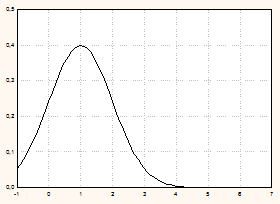
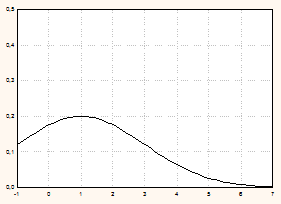
График плотности нормального распределения называют нормальной кривой (кривой Гаусса). Эта кривая симметрична относительно вертикальной оси, проходящей через точку x=a, и имеет в этой точке единственный максимум, равный 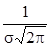. С уменьшением s кривая становится все более островершинной. Изменение a при неизменном s приводит к смещению кривой по оси абсцисс. (Графики плотности нормального распределения при различных параметрах см. на рис. 5.10).

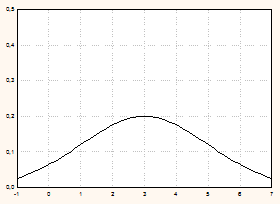
a =3, s=1	a =3, s=2
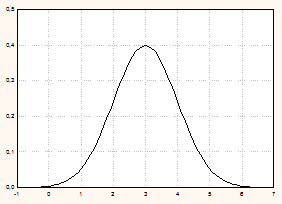
a =1, s=1	a =1, s=2

Рис. 5.10.

При a=0 и s=1 нормальную кривую называют нормированной.

Нормированная СВ – СВ X*, связанная с исходной СВ X линейным преобразованием: X*=(X - М X)/ .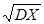

Обозначают нормированную СВ – N(0,1).

Плотность нормированной СВ определяется по формуле .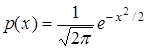

Поскольку непосредственное вычисление функции распределения случайной величины, имеющей нормальное распределение, затруднено (ее выражение содержит «неберущийся» интеграл), для ее нахождения используются табличные значения функции Лапласа [5] – .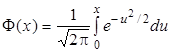

Заметим, что таблицы построены лишь для положительных х и для х=0. Для отрицательных значений х следует использовать нечетность функции Ф(х) (Ф(-х) = -Ф(х)). При x>5 можно принять Ф(х)=0,5.

При этом функция распределения (F_N) СВ, распределенной по нормальному закону с параметрами 0 и 1, выражается через функцию Лапласа следующим образом: .

Геометрически функция Лапласа представляет собой площадь под стандартной нормальной кривой на отрезке [0, x].

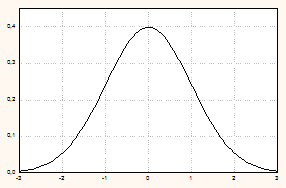
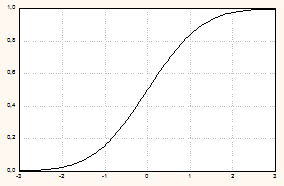
Графики нормированной нормальной кривой и функции распределения нормированной СВ см. на рис. 5.11.

Нормированная нормальная кривая	Функция распределения нормированной СВ

Рис. 5.11.