Застосування рядів до розв'язування диференціальних рівнянь

Нехай потрібно про інтегрувати диференціальне рівняння другого порядку

(1)

Якщо його розв'язок не виражається через елементарні функції в кінцевому вигляді або звичайні способи розв’язування дуже трудомісткі, то в окремих випадках його розв'язок (частинний або загальний) вдається відшукати у вигляді деякого степеневого ряду.

Спосіб послідовних диференціювань застосовується, коли потрібно знайти частинний розв'язок 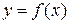рівняння (1), що задовольняє початковим умовам

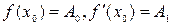. (2)

Якщо в околі точки рівняння (1) задовольняє умовам теореми існування і єдиності розв'язку задачі Коші для диференціального рівняння другого порядку, то можна спробувати шукати його частинний розв'язок у у вигляді ряду Тейлора

(3)

перші два члени якого відомі, оскільки .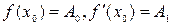

З рівняння (1) знаходимо . Якщо потім про диференціювати рівняння (1) за змінною 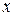, то можна послідовно знайти скільки завгодно похідних шуканої функції в точці :

.

Тут під символами .розуміються повні похідні за змінною 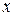від функції в припущенні, що і залежать від 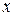, тобто

і т.д. Після підстановки знайдених похідних функції в розвинення (2), одержуємо невідомий розв'язок

Розглянутий метод може бути застосований і для розв’язання диференціальних рівнянь будь-якого порядку.