Ряді Фур'є

Теорема. Якщо функція розвинута в рівномірно збіжний на всій числовій вісі тригонометричний ряд

, (1)

то коефіцієнти цього ряду визначаються формулами

(2)

Теорема справедлива і у тому випадку, коли функція визначена лише на відрізку або всякому іншому відрізку довжини 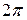, а тригонометричний ряд збігається на цьому відрізку рівномірно. При цьому границі інтегрування у формулах замінюються відповідно на і . З формул (2) слідує, що формально для всякої інтегрованої на відрізку функції можна скласти ряд (1). Ряд (1), коефіцієнти якого визначаються формулами (2) незалежно від того, збігається він до функції чи ні, називається рядом Фур'є для функції ; це записується так:

. (3)

Коефіцієнти , визначені формулами (1), називаються коефіцієнтами Фур'є.

З формул (2) слідує, що формально для всякої інтегрованої на відрізку функції можна скласти ряд (1). Проте між функцією і цим рядом не завжди можна поставити знак рівності. Теорема Діріхле дає достатні умови розвинення функції в ряд Фур'є.

Теорема Діріхле. Якщо періодична функція має період 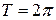і є кусково-гладкою (на кожному с кінченому інтервалі вона і її похідна мають не більше скінченого числа точок розриву першого роду) або кусково-монотонною, то в кожній точці безперервності функція розвинена в ряд Фур'є, причому цей ряд збігається і в кожній точці розриву функції до середнього арифметичного правої і лівої границь функції в точці , тобто до числа .

У ряд Фур'є можна розкласти і неперіодичну кусково-гладку функцію , задану лише в інтервалі . При цьому одержаний ряд збігатиметься до функції тільки в тих точках інтервалу , в яких функція неперервна. Одержаний ряд буде збіжним на всій числовій вісі, а його сумою буде періодичне продовження функції на всю вісь . Виняток становитимуть лише точки розриву, в яких сума ряду буде дорівнювати середньому арифметичному правої і лівої границь періодичного продовження даної функції.

Періодичним продовженням називається функція , співпадаюча в інтервалі і що задовольняє для кожного 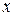умові .

Розглянемо окремі випадки розвинення функції в тригонометричний ряд Фур'є.

1. Якщо – парна функція , то функція буде також парною, а функція – непарною. Отже, маємо:

а тому

.

2. Якщо – непарна функція , то функція буде також непарною, а функція – парною. Отже

тому розкладання приймає вигляд

.

Зауваження. 1.Функція, задана в інтервалі 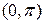, може бути розкладена залежно від вимог або в ряд тільки косинусів, або в ряд тільки синусів. Для цього вона повинна бути продовжена в інтервалі 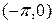або як парна, або як непарна.

2.Функція, задана в інтервалі 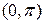, може бути розкладена в ряд Фур'є нескінченним числом способів, дивлячись за тим, як побудовано продовження в інтервалі .