 |
Главная Случайная страница Контакты | Мы поможем в написании вашей работы! | |
Завдання 11
|
|
Зобразити інтегралом Фур'є в комплексній формі функцію

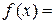

Розв’язання: За формулою (5.19) [1, с. 316] маємо

 .
.
Перший та останній інтеграли дорівнюють нулю, оскільки дорівнює нулю підінтегральна функція. Обчислимо окремо другий та третій інтеграли.

 .
.

 .
.
Тоді

 .
.
Застосовуючи формулу (5.18) [1, с. 316], маємо
 .
.
Задана функцію неперервну в усіх точках, окрім тих, в яких вона змінює свій аналітичний вираз. Перевіримо також неперевність і в цих точках.
1) 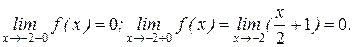 Так як
Так як  , то функція
, то функція 
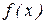 неперервна в точці
неперервна в точці 
 Так як
Так як  , то функція
, то функція 
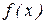 неперервна в точці
неперервна в точці  1
1  )
) 
 Так як
Так як  , то функція
, то функція 
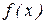 неперервна в точці
неперервна в точці 
Отже, функція 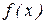 неперервна при всіх
неперервна при всіх 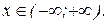 З умови також видно що функція є кусково-гладкою. Отже інтеграл Фур'є для функції
З умови також видно що функція є кусково-гладкою. Отже інтеграл Фур'є для функції 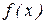 дорівнює функції
дорівнює функції 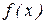 при всіх
при всіх 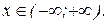 і
і
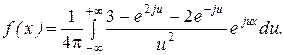
Відповідь: 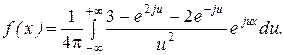
Дата публикования: 2014-10-20; Прочитано: 524 | Нарушение авторского права страницы | Мы поможем в написании вашей работы!
