 |
Главная Случайная страница Контакты | Мы поможем в написании вашей работы! | |
Зразок виконання розрахунково-графічної роботи №5 за
|
|
темою " Ряди"
Завдання 1. Дослідити на збіжність ряди з додатними членами:
а) 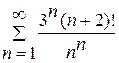
Розв’язання: за ознакою Даламбера [1, с. 238—240], маємо:


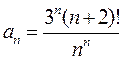
 ;
; 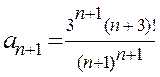
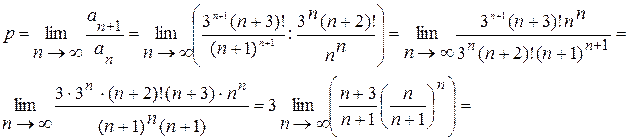
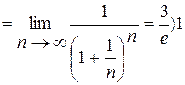
Так як 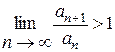 , то цей ряд за ознакою Д'Аламбера розбігається.
, то цей ряд за ознакою Д'Аламбера розбігається.
Відповідь: ряд розбігається.
б) 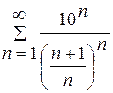
Розв’язання: за ознакою Коші [1, с. 242], маємо:
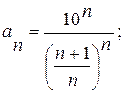
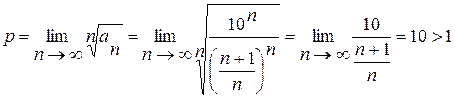 .
.
Так як 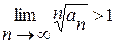 , то цей ряд за ознакою Коші розбігається.
, то цей ряд за ознакою Коші розбігається.
Відповідь: ряд розбігається.
Користуючись ознаками порівняння, дослідити на збіжність ряди:
в) 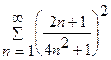
Розв’язання
Дослідимо цей ряд за допомогою граничної ознаки порівняння [1, с. 237]
За ряд, з яким будемо порівнювати даний ряд, візьмемо узагальнений гармонічний збіжний ряд 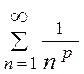 . Маємо
. Маємо 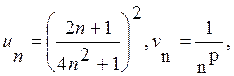

Для того, щоб можна було скористатися граничною ознакою порівняння треба щоб границя була скінченою і ненульовою. Це виконується, коли степені чисельника та знаменника рівні. Отже, обираємо 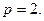 Тоді
Тоді 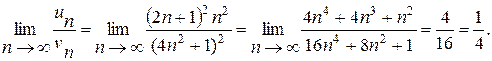
Оскільки отримали скінчену ненульову границю, то обидва ряди мають однакову збіжність. Узагальнений гармонічний ряд при 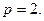 збігається. Отже, заданий ряд також є збіжний.
збігається. Отже, заданий ряд також є збіжний.
Відповідь: ряд збігається.
г) 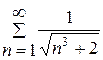
Розв`язання: будемо користуватися ознакою порівняння [1, с. 234]. За ряд, з яким будемо порівнювати даний ряд, візьмемо узагальнений гармонічний ряд
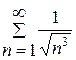 .
.
Для даних рядів виконується нерівність: 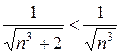 ;
; 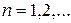
Так як узагальнений гармонічний ряд 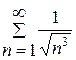 збігається (р=⅔>1, [1, с. 245]), то ряд
збігається (р=⅔>1, [1, с. 245]), то ряд 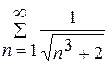 також збігається за ознакою порівняння.
також збігається за ознакою порівняння.
Відповідь: ряд збігається.
д) 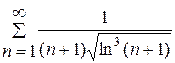
Розв’язання: розглянемо функцію 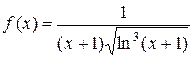 . Ця функція є додатною, нерозривною та монотонно спадає при
. Ця функція є додатною, нерозривною та монотонно спадає при 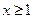 . Тому можливо досліджувати цей ряд на збіжність, користуючись інтегральною ознакою збіжності [1, с. 243]. Для цього необхідно дослідити на збіжність невласний інтеграл
. Тому можливо досліджувати цей ряд на збіжність, користуючись інтегральною ознакою збіжності [1, с. 243]. Для цього необхідно дослідити на збіжність невласний інтеграл
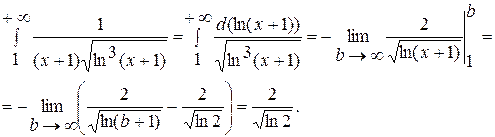
Так як невласний інтеграл збігається, то даний ряд також збігається.
Відповідь: ряд збігається.
Завдання 2. Дослідити на збіжність та абсолютну збіжність знакопереміжний ряд
 .
.
Розв’язання: Оскільки заданий ряд є знакопереміжним, то можемо скористатися ознакою Лейбніця
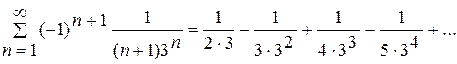 .
.
Абсолютні значення членів даного знакопереміжного ряда зменшуються:
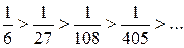 і, крім того,
і, крім того,
 .
.
Тому, за ознакою Лейбніца, [1, с.246], цей ряд збігається. Визначимо, як збігається даний ряд: абсолютно чи умовно. Для цього складемо ряд з абсолютних величин членів даного ряду 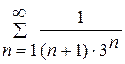 та дослідимо його на збіжність за допомогою ознаки Даламбера [1, с.238—240].
та дослідимо його на збіжність за допомогою ознаки Даламбера [1, с.238—240].
Маємо
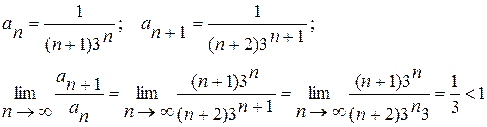
Так як 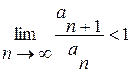 , то даний ряд збігається. Таким чином, даний знакопереміжний ряд збігається абсолютно.
, то даний ряд збігається. Таким чином, даний знакопереміжний ряд збігається абсолютно.
Відповідь: ряд збігається абсолютно.
Завдання 3. Знайти область збіжності степеневого ряду.
а) 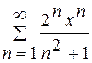
Роз’язання. Знайдемо радіус збіжності ряду за формулою (2.71) [1, с.241]: 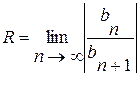 . Для даного ряду
. Для даного ряду
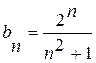 ;
; 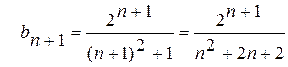 .
.
Маємо 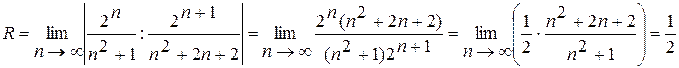 Отже, даний ряд збігається при
Отже, даний ряд збігається при 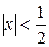 .Тоді інтервал збіжності
.Тоді інтервал збіжності 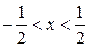 .
.
Тепер дослідимо поведінку ряду у точках 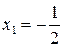 й
й 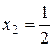 . Підставимо в данний ряд замість x значення
. Підставимо в данний ряд замість x значення 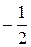 . Одержимо ряд
. Одержимо ряд 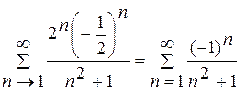 . Дослідимо цей знакопереміжний ряд на збіжність за ознакою Лейбніця [1, с.246]. Для нього виконуються наступні умови:
. Дослідимо цей знакопереміжний ряд на збіжність за ознакою Лейбніця [1, с.246]. Для нього виконуються наступні умови:
1) 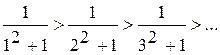 2)
2) 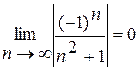 .
.
Умови ознаки Лейбніця виконані.Отже при 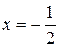 даний степеневий ряд збігається.
даний степеневий ряд збігається. 
При 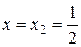 дістаємо ряд
дістаємо ряд 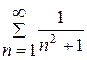 . Порівняємо його з рядом Діріхле
. Порівняємо його з рядом Діріхле 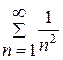 , який збігається при
, який збігається при 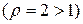 . Так як
. Так як 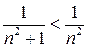 , то за ознакою порівняння [1, с.237] ряд
, то за ознакою порівняння [1, с.237] ряд 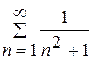 збігається.
збігається.
Відповідь: область збіжності 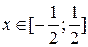 .
.
б) 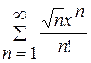 .
.
Розв’язання:
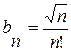 ;
; 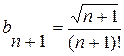 .
.
Отже:  . Даний ряд збігається на усій числовій осі, тобто,
. Даний ряд збігається на усій числовій осі, тобто, 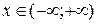 .
.
Відповідь: область збіжності 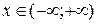 .
.
в) 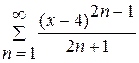 .
.
Розв'язання: Коефіцієнти цього ряду при парних степенях 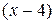 дорівнюють нулю. Тому ми не можемо скористатися безпосередньо формулами (2.71)
дорівнюють нулю. Тому ми не можемо скористатися безпосередньо формулами (2.71)
[1, с.241]. Винесемо спільний множник 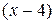 за знак суми.
за знак суми.
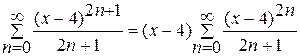
Скористаємося ознакою Даламбера.

За ознакою Даламбера ряд збігається при 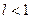 й розбігається при
й розбігається при 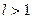 . Для знаходження точок збіжності розв'яжемо нерівність
. Для знаходження точок збіжності розв'яжемо нерівність 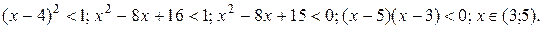
При виконанні умови 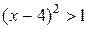 даний ряд розбігається. Ця нерівність виконується при
даний ряд розбігається. Ця нерівність виконується при 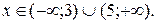 Отже інтервалом збіжності є
Отже інтервалом збіжності є 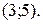
Дослідимо на збіжність цей ряд в кінцях інтервалу збіжності.
Нехай 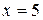 . Маємо ряд
. Маємо ряд 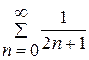 . За допомогою ознаки порівняння у граничній формі даний ряд порівняємо з розбіжним гармонічним рядом
. За допомогою ознаки порівняння у граничній формі даний ряд порівняємо з розбіжним гармонічним рядом 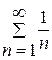 .
. 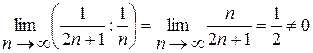 . Отже, обидва ряди мають однакову збіжність і при
. Отже, обидва ряди мають однакову збіжність і при 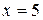 степеневий ряд
степеневий ряд 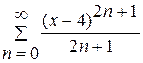 розбігається. Нехай
розбігається. Нехай 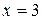 . Тоді маємо знакосталий ряд
. Тоді маємо знакосталий ряд 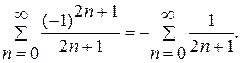 Оскільки ряд
Оскільки ряд 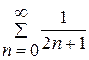 розбігається, то і
розбігається, то і
ряд - 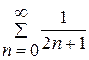 також розбіжний (що виходить з теореми 1[1, с.226]).
також розбіжний (що виходить з теореми 1[1, с.226]).
Відповідь: 
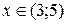
Завдання 4. а) Розвинути в ряд Маклорена функцію 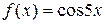 .Вказати область збіжності отриманого ряду до цієї функції.
.Вказати область збіжності отриманого ряду до цієї функції.
Розв'язання. Замінюючи в розкладанні (2.114) [1,с.265] 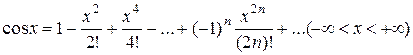
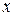 на
на 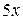 .
.
Маємо 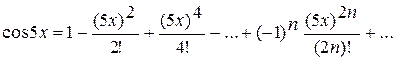 ,
, 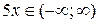
або 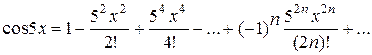 ,
, 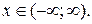
Відповідь: 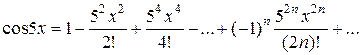 ,
, 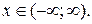
б) Розвинути функцію 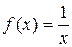 у ряд Тейлора в околі точки
у ряд Тейлора в околі точки 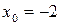 . Знайти область збіжності здобутого ряду.
. Знайти область збіжності здобутого ряду.
Розв'язання: Для розв'язання даної задачі скористаємося формулою суми нескінченої геометричної прогресії при 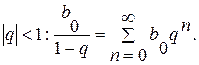
Отже 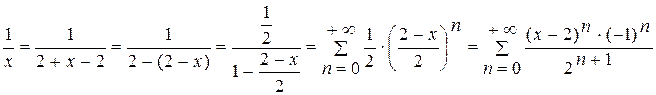 при
при 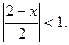
Остання нерівність виконується при 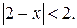 Тобто
Тобто 
Відповідь: 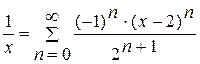 ; область збіжності
; область збіжності 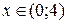 .
.
Завдання 5. За допомогою розвинення у степеневий ряд обчислити 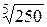 з точністю до
з точністю до 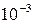 .
.
Розв’язання. Для обчислення скористаємося біноміальним рядом 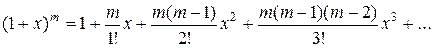 , де
, де 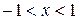 (формула (2.115) [1,с.266]). Заданий вираз перепишемо у вигляді:
(формула (2.115) [1,с.266]). Заданий вираз перепишемо у вигляді: 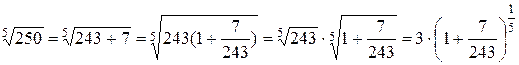 .
.
Вважаючи 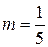 ;
; 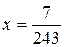 , одержуємо
, одержуємо
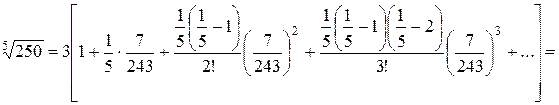
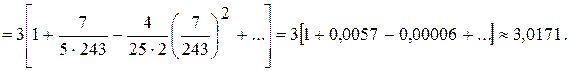 Знаки членів одержаного числового ряду чергуються, починаючи з другого члену. Обмежившись першими n доданками припустимо похибку, модуль якої за наслідком ознаки Лейбніца не перевищує модуля першого відкинутого члена. Оскільки модуль третього члена ряду менш за
Знаки членів одержаного числового ряду чергуються, починаючи з другого члену. Обмежившись першими n доданками припустимо похибку, модуль якої за наслідком ознаки Лейбніца не перевищує модуля першого відкинутого члена. Оскільки модуль третього члена ряду менш за 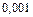 , то ми можемо залишити тільки перші два доданки.
, то ми можемо залишити тільки перші два доданки.
Відповідь:. 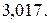
Завдання 6. Використовуючи розвинення підінтегральної функції в степеневий ряд, обчислити визначний інтеграл з точністю до 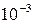 .
.
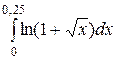 .
.
Роз’в'язання: Використаємо розвинення в ряд функції 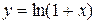 :
: 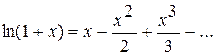 . Ряд справа збігається рівномірно на кожному відрізку
. Ряд справа збігається рівномірно на кожному відрізку 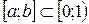 , зокрема на відрізку
, зокрема на відрізку 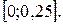
 Проінтегруємо обидві частини рівності.
Проінтегруємо обидві частини рівності. 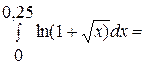

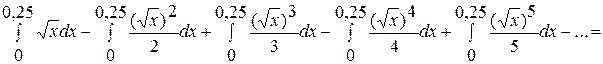
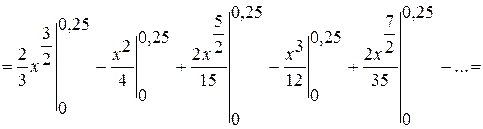
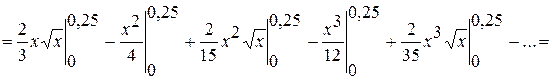 0,08333-0,015625+0,004166-0,001302+0,000446-... Одержали знакопереміжний числовий ряд, модулі членів якого спадають. Знаки членів одержаного ряду чергуються, починаючи з першого члену. Оскільки модуль п'ятого члену ряду менш за
0,08333-0,015625+0,004166-0,001302+0,000446-... Одержали знакопереміжний числовий ряд, модулі членів якого спадають. Знаки членів одержаного ряду чергуються, починаючи з першого члену. Оскільки модуль п'ятого члену ряду менш за 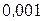 , то залишимо тільки перші чотири доданки. Тому маємо, що.
, то залишимо тільки перші чотири доданки. Тому маємо, що. 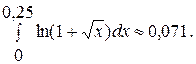
Відповідь: 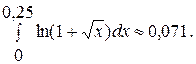
Завдання 7. Методом послідовного диференціювання знайти перші k ненульових членів розвинення в степеневий ряд розв’язку рівняння при даних початкових умовах:
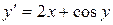 ,
, 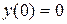 , k= 5.
, k= 5.
Розв'язання: Шукаємо розв'язок у вигляді

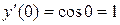
Знайдемо другу, третю, четверту і п’яту похідні функції і обчислимо їх для х=0:
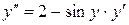 ;
; 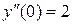
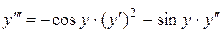 ;
; 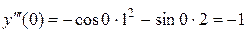 ;
;
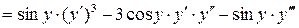 ;
; 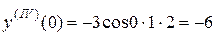 .
. 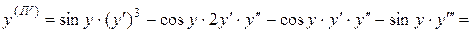
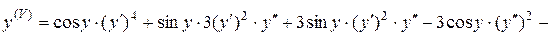
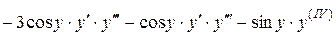 ;
;
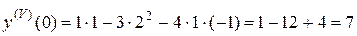 .
.
Тоді розв’язок буде мати вигляд:
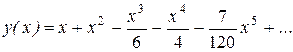
Відповідь: 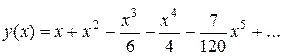
Завдання 8. Розвинути в ряд Фур'є періодичну з періодом 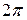 функцію
функцію
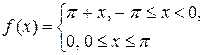
Розв'язання. Обчислимо коефіцієнти ряду Фур'є за формулами (3.5),(3.8), (3.9) [1,с.281,с.282]:

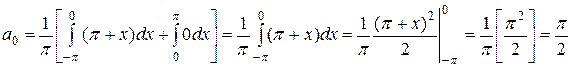 ;
; 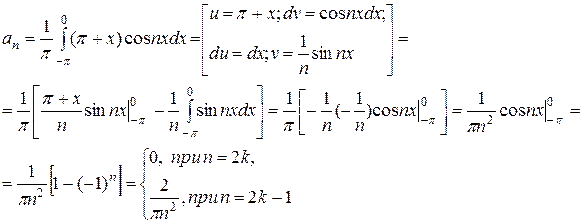

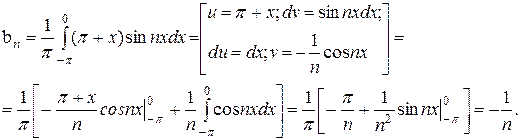
Отже, підставляючи коефіцієнти 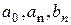 у формулу (3.4) [1, с. 280] одержимо
у формулу (3.4) [1, с. 280] одержимо
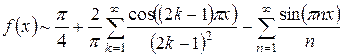
Завдання 9. Розвинути в ряд Фур'є функцію 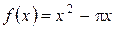 , задану в інтервалі
, задану в інтервалі 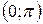 , до визначивши її парним та непарним способом.
, до визначивши її парним та непарним способом.
Розв’язання.
а)Продовжимо дану функцію на 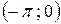 парним способом.У цьому випадку ряд Фур'є має вигляд
парним способом.У цьому випадку ряд Фур'є має вигляд
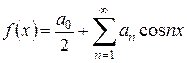 ,
, 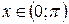 ,
,
де коефіцієнти 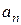 обчислюються за формулами (3.12), (3.13) [1, с.285].
обчислюються за формулами (3.12), (3.13) [1, с.285].
Знаходимо:
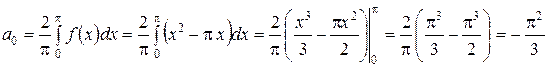 ;
;
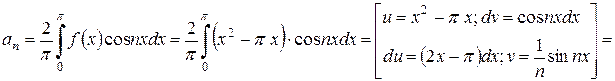
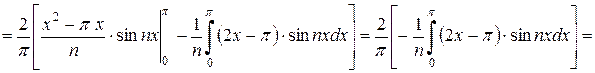
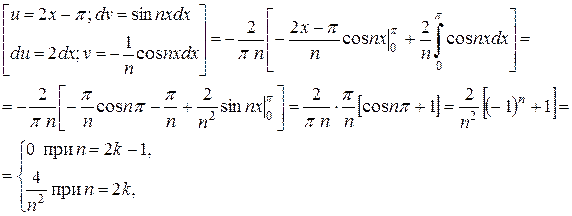
де 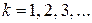
Підставляючи коефіцієнти в ряд Фур'є, маємо:
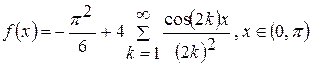 .
.
б)Продовжимо дану функцію 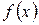 на
на 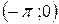 непарним способом
непарним способом
У цьому випадку ряд Фур'є має вигляд:
 де
де 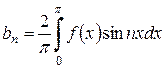 .
.
Маємо


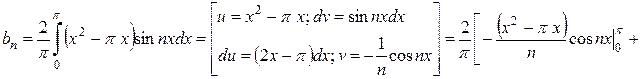
Одержимо
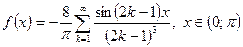 .
.
Завдання 10. Розвинути в ряд Фур¢є функцію 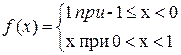
(з періодом 
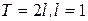 ).
).
Розв¢язання. Обчислимо коефіцієнти ряду Фур¢є:
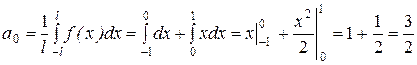 ;
;
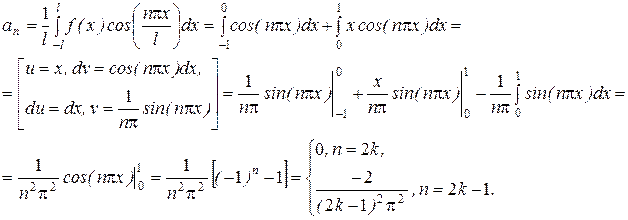
Отже,
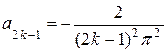 ,
, 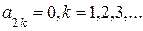
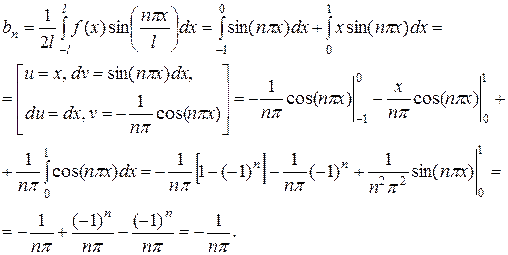
Одержимо
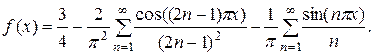
Дата публикования: 2014-10-20; Прочитано: 3318 | Нарушение авторского права страницы | Мы поможем в написании вашей работы!
