Числові ряди

|лави,низки|

Нехай|нехай| задана послідовність чисел 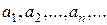. Якщо ці числа з'єднати знаками “+”, то вийде вираз|вираження| вигляду|виду|

,

що називається числовим рядом|лавою,низкою| і скорочено позначається|значиться| символом

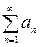. (1)

Числа 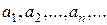називаються членами ряду|лави,низки|; 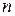-й член ряду|лави,низки| називається також загальним|спільним| членом ряду|лави,низки|. Ряд|лава,низка| вважається|лічиться| заданим, якщо задано правило, що дозволяє за відомим номером члену 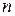записати член цього ряду|лави,низки|. Найчастіше ряд|лава,низка| задається формулою загального|спільного| члена .

Сума 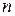перших членів ряду|лави,низки| називається 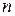-й частковою сумою ряду|лави,низки| і позначається|значиться| символом :

.

Якщо існує|скінченна| границя , то ряд|лава,низка| називається збіжним, а число 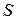– сумою ряду|лави,низки|. В цьому випадку пишуть

.

Таким чином, символом (1) позначається|значиться| як сам ряд|лава,низка|, так і його сума.

Ряд|лава,низка| називається розбіжним, якщо границя не існує (зокрема, якщо ).

Ряд|лава,низка|

,

одержаний|отриманий,набутий| з|із| ряду|лави,низки| (1) відкиданням перших його членів, називається -м залишком|остачею| ряду|лави,низки| (1).

Якщо сума залишку|остачі| збіжного ряду|лави,низки| позначити , то .

|слідуючі| Теореми:

1. Відкидання від ряду|лави,низки| або приєднання до ряду|лави,низки| будь-якого скінченого|скінченного| числа членів не змінює|змінює,замінює| його збіжності або розбіжності|.

2. Для того щоб ряд|лава,низка| (1) збігався необхідно і достатньо щоб границя його m- го| залишку|остачі| при дорівнювала нулю, тобто .

3. Якщо члени збіжного ряду|лави,низки| (1), який має суму 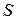, помножити на число , то одержаний|отриманий,набутий| ряд |лава,низка| буде також збіжним, а число – його сумою.

4. Множення членів розбіжного ряду|лави,низки| на число не порушує його розбіжністі|.

5. Необхідна ознака збіжності ряду|лави,низки|. Якщо ряд|лава,низка| (1) збігається, то границя його загального|спільного| члена дорівнює нулю:

Звідси випливає, що якщо 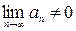, то ряд|лава,низка| розбігається. Якщо ж , то про збіжність ряду|лави,низки| ще нічого не можна сказати, але|та| є сенс|зміст,рація| досліджувати ряд|лаву,низку| далі.